.
Замечания: 1. Как следует из определений 1 и 2, соответственно, запись 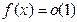 (при
(при  ) означает, что функция
) означает, что функция  – бесконечно малая при
– бесконечно малая при  , а запись
, а запись 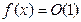 (при
(при  ) означает, что функция
) означает, что функция  ограничена в окрестности точки
ограничена в окрестности точки 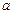 .
.
2. Если 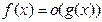 при
при  , то в силу теоремы о локальной ограниченности функции, имеющей (конечный) предел, тем более
, то в силу теоремы о локальной ограниченности функции, имеющей (конечный) предел, тем более 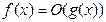 при
при  .
.
Упражнение 1. Покажите, что (функции  и
и 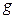 – функции одного порядка) ⇔ (
– функции одного порядка) ⇔ (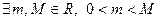 ,
, 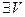 - окрестность точки
- окрестность точки 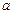 , что
, что 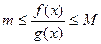 при
при 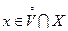 ).
).
Определения: 5. Пусть  и
и 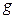 – бесконечно малые при
– бесконечно малые при  функции. Функция
функции. Функция  называется бесконечно малой высшего порядка по сравнению с функцией
называется бесконечно малой высшего порядка по сравнению с функцией 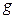 , если
, если 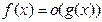 при
при  .
.
6. Если бесконечно малые при  функции
функции  и
и 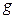 асимптотически равны, то говорят, что они эквивалентны при
асимптотически равны, то говорят, что они эквивалентны при  ,при этом пишут
,при этом пишут  ~
~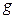 (
( ).
).
Теорема 1. Пусть 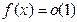 и
и 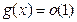 при
при  . Тогда
. Тогда
[ ~
~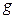 (
( )] ⇔ [
)] ⇔ [ 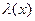 ≜
≜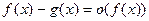 при
при  ]
]
Д о к а з а т е л ь с т в о. Необходимость (⇒). Так как  ~
~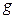 (
( ), то
), то
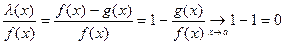 ,
,
т.е. 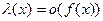 при
при  .
.
Достаточность (⇐). Поскольку 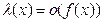 при
при  , то
, то
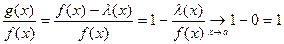 ,
,
т.е.  ~
~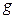 (
( ) □
) □
Теорема 2. Пусть 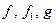 и
и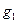 – бесконечно малые при
– бесконечно малые при  функции, причем
функции, причем  ~
~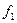 , а
, а 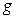 ~
~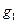 при
при  . Тогда если
. Тогда если
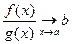 ,
,
то и
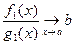 .
.
Замечание 3. Иными словами в этой теореме утверждается, что при отыскании предела частного бесконечно малых функций, каждую из этих бесконечно малых можно заменить на эквивалентную бесконечно малую.
Д о к а з а т е л ь с т в о теоремы 2. Поскольку
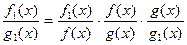
и по условию
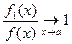 ,
,
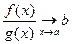 ,
,
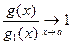 ,
,
то по теореме о пределе частного имеем
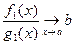 □
□
По аналогии с определениями 5 и 6 вводятся следующие определения для бесконечно больших функций.
Определения: 7. Пусть  и
и 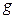 – бесконечно большие при
– бесконечно большие при  функции. Функция
функции. Функция  называется бесконечно большой высшего порядка по сравнению с функцией
называется бесконечно большой высшего порядка по сравнению с функцией 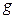 , если
, если 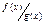 – бесконечно большая при
– бесконечно большая при  функция, т.е. если
функция, т.е. если 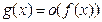 при
при  .
.
8. Если бесконечно большие при  функции
функции  и
и 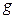 асимптотически равны при
асимптотически равны при  , то говорят, что они эквивалентны при
, то говорят, что они эквивалентны при  .
.
Замечание 4. Теоремы 1 и 2 при надлежащих изменениях сохраняют свою силу для бесконечно больших функций.
Определение 9. Пусть  и
и 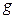 – бесконечно малые (бесконечно большие) при
– бесконечно малые (бесконечно большие) при  функции. Если
функции. Если 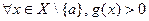 и функции
и функции 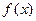 и
и 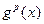 одного порядка при
одного порядка при  (здесь
(здесь 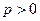 ), то говорят, что
), то говорят, что  – бесконечно малая (бесконечно большая) порядка
– бесконечно малая (бесконечно большая) порядка 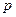 по сравнению
по сравнению 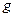 .
.
Определение 10. Пусть  и
и 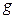 – бесконечно малые (бесконечно большие) при
– бесконечно малые (бесконечно большие) при  функции. Если
функции. Если 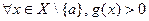 и
и 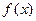 ~
~ 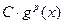 при
при  , то говорят, что функция
, то говорят, что функция  (при сравнении с
(при сравнении с 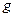 ) имеет главную часть
) имеет главную часть 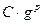
Определение 1. Функция 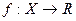 ,
, 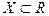 , называется непрерывной в точке
, называется непрерывной в точке 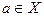 , если для любого
, если для любого 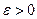 существует такое
существует такое 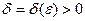 , что для любого
, что для любого 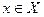 , удовлетворяющего неравенству
, удовлетворяющего неравенству
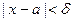 , ,
| (1) |
справедливо также и неравенство
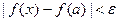
| (2) |
Замечание 1. Данное определение иногда называется определением непрерывности функции на языке 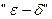 . По форме оно явно напоминает определение предела функции в форме Коши, при этом в отличие от него здесь требуется, чтобы точка
. По форме оно явно напоминает определение предела функции в форме Коши, при этом в отличие от него здесь требуется, чтобы точка 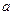 принадлежала множеству
принадлежала множеству 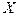 , но не требуется, чтобы она была точкой сгущения этого множества.
, но не требуется, чтобы она была точкой сгущения этого множества.
В связи с последним замечанием отметим, что если точка 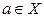 не является точкой сгущения множества
не является точкой сгущения множества 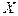 , то она называется изолированной точкой этого множества. Иными словами точка
, то она называется изолированной точкой этого множества. Иными словами точка 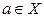 называется изолированной точкой множества
называется изолированной точкой множества 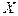 , если существует такая ее окрестность
, если существует такая ее окрестность 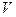 , что
, что 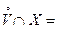 Æ или, что тоже самое,
Æ или, что тоже самое, 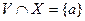 .
.
Замечание 2. Согласно определению 1 в любой изолированной точке своей области определения всякая функция является непрерывной. Действительно, каково бы ни было 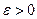 по определению изолированной точки можно выбрать столь малое
по определению изолированной точки можно выбрать столь малое 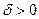 , что
, что 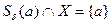 и, следовательно, при этом
и, следовательно, при этом 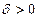 среди точек множества
среди точек множества 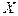 неравенству (1) будет удовлетворять только точка
неравенству (1) будет удовлетворять только точка 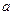 , но для
, но для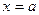 неравенство (2) очевидно выполняется для любой функции
неравенство (2) очевидно выполняется для любой функции  .
.
Замечание 3. В силу того, что для 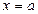 неравенство (2) выполняется очевидным образом, можно заключить, что в том случае, когда точка
неравенство (2) выполняется очевидным образом, можно заключить, что в том случае, когда точка 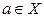 является точкой сгущения множества
является точкой сгущения множества 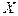 , неравенство (1) можно заменить неравенствами:
, неравенство (1) можно заменить неравенствами: 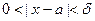 , при этом определение 1 превратится в определение предела
, при этом определение 1 превратится в определение предела 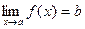 при
при 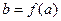 . Таким образом, можно сказать, что если точка
. Таким образом, можно сказать, что если точка 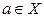 является точкой сгущения множества
является точкой сгущения множества 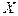 , то функция
, то функция  будет непрерывной в этой точке в том и только том, случае, когда
будет непрерывной в этой точке в том и только том, случае, когда 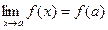 .
.
Замечание 4. На языке окрестностей определение 1 можно переформулировать следующим образом:
Определение 1’. Функция 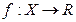 ,
, 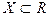 , называется непрерывной в точке
, называется непрерывной в точке 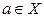 , если для любого
, если для любого 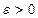 существует такое
существует такое 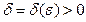 , что
, что
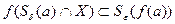
(т.е. 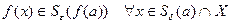 ).
).
Это определение, а значит и определение 1, очевидно равносильно следующему определению:
Определение 1”. Функция 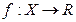 ,
, 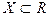 , называется непрерывной в точке
, называется непрерывной в точке 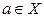 , если для любой окрестности
, если для любой окрестности 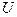 точки
точки 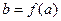 существует такая окрестность
существует такая окрестность 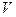 точки
точки 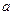 , что
, что
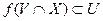 .
.
С учетом замечаний 2 и 3, теоремы о равносильности определений предела по Коши и по Гейне, а также с учетом того, что всякую точку 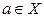 можно представить в виде
можно представить в виде 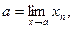
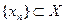 ,*) заключаем, что определения 1 и 1’ равносильны следующему определению:
,*) заключаем, что определения 1 и 1’ равносильны следующему определению:
Определение 2. Функция 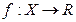 ,
, 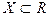 , называется непрерывной в точке
, называется непрерывной в точке 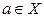 , если для любой последовательности точек
, если для любой последовательности точек 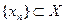 ,
, 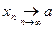 , последовательность
, последовательность 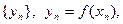 сходится и
сходится и
 2014-02-09
2014-02-09 765
765