Полярные координаты

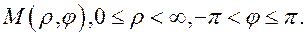
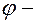 величина направленного угла.
величина направленного угла.
Задача. Назовите координатные линии полярной системы.
Установим связь между полярными и декартовыми прямоугольными координатами точки. Для этого к полярной системе присоединим репер
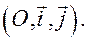 Пусть
Пусть 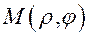 и
и 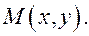
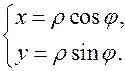 (9)
(9)
Обратно: 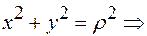
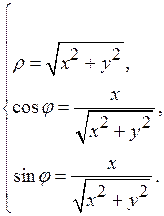 (10)
(10)
или 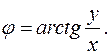
Введение системы координат на плоскости позволяет использовать
при решении задач метод координат. При использовании этого метода каждая фигура задается с помощью уравнения или неравенства. При этом мы имеем дело с аналитическим методом решения задачи, а геометрия называется аналитической. В ней решаются две задачи:
1) по заданным свойствам фигуры составить аналитические условия, её определяющие;
2)по аналитическим свойствам, задающим фигуру, исследовать её свойства.
Очень часто на плоскости рассматривают геометрическую фигуру, называемую линией. Она задается своим уравнением: уравнение, которому удовлетворяют координаты любой точки этой линии и не удовлетворяют координаты посторонней точки.
Опр. Линия на плоскости называется алгебраической, если в некоторой аффинной системе координат её уравнение можно представить в виде 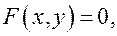 где
где 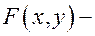 многочлен от переменных
многочлен от переменных 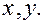
Степень этого многочлена называется порядком линии.
Примеры: 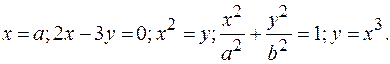
Задача. Записать уравнение окружности с центром в точке 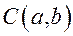 и радиусом
и радиусом 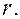
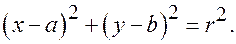
Это линия 2-го порядка.
Частный случай: 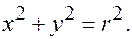
Примеры неалгебраических линий: 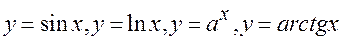 и т.д.
и т.д.
Задача. При каких условиях на коэффициенты уравнение
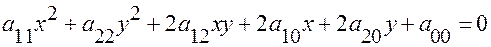 определяет окружность в дпск?
определяет окружность в дпск?
Задача. Определите координаты центра и радиус окружности
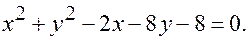
 2014-02-09
2014-02-09 1076
1076








