4.1. Различные уравнения прямой в пространстве.
 4.1.1. Канонические уравнения прямой в пространстве.
4.1.1. Канонические уравнения прямой в пространстве.
Положение прямой однозначно определяется,
если известна одна её точка 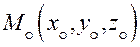
и направляющий вектор 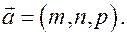 По
По
этим данным составим уравнения прямой.
Возьмем на прямой произвольную точку 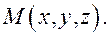 Векторы
Векторы 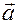 и
и
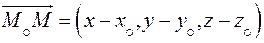 коллинеарны, отсюда:
коллинеарны, отсюда:
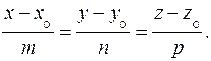 (13)
(13)
Это канонические уравнения прямой в пространстве.
4.1.2. Уравнения прямой, проходящей через две точки.
Две точки 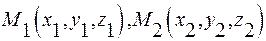 прямой определяют её направляющий вектор
прямой определяют её направляющий вектор 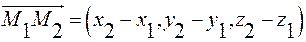 . По формуле (13) получим искомые уравнения:
. По формуле (13) получим искомые уравнения:
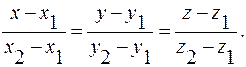 (14)
(14)
4.1.3. Параметрические уравнения прямой.
Они получаются из канонических:
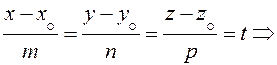
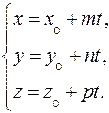 (15)
(15)
Задавая параметру 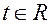 различные значения, получим координаты различных точек прямой.
различные значения, получим координаты различных точек прямой.
4.1.4. Общие уравнения прямой.
Прямая может быть получена как линия пересечения двух плоскостей:
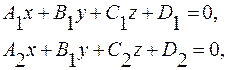 (16)
(16)
если
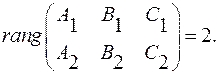
Уравнения (16) называются общими уравнениями прямой в пространстве.
Получим канонические уравнения этой прямой. Возьмем на ней какую-нибудь точку 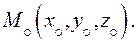 Направляющий вектор в дпск есть векторное произведение нормальных векторов данных плоскостей:
Направляющий вектор в дпск есть векторное произведение нормальных векторов данных плоскостей:
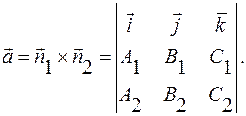 Окончательно получим:
Окончательно получим:
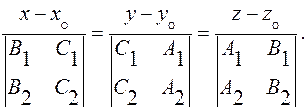
Задача. Определите точку пересечения прямой
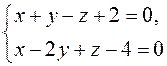 с плоскостью
с плоскостью 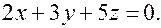
4.2.Взаимное расположение двух прямых.
Зададим в аффинной системе координат 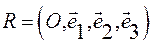 две прямые:
две прямые: 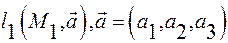 и
и 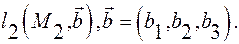
По направляющим векторам 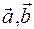 и вектору
и вектору 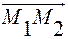 можно определить
можно определить
взаимное расположение данных прямых. Возможны 4 случая: 1) прямые скрещиваются, 2) прямые пересекаются, 3) прямые параллельны,4)прямые совпадают.
Очевидно, прямые лежат в одной плоскости тогда и только тогда, когда векторы 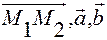 компланарны.
компланарны.
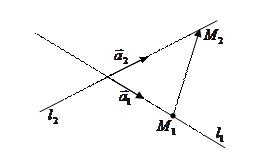 Тогда их смешанное произведение равно 0:
Тогда их смешанное произведение равно 0:
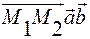 =0 (17)
=0 (17)
1) Прямые скрещиваются тогда и только
тогда, когда
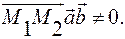 (18)
(18)
2) Прямые пересекаются тогда и только тогда, когда они лежат в одной плоскости, то есть выполнено условие (17), и векторы 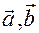 коллинеарны.
коллинеарны.
3) Прямые, лежащие в одной плоскости, параллельны, если они не имеют общих точек. При этом векторы удовлетворяют условиям:
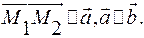 (19)
(19)
4) Ясно, что прямые совпадают тогда и только тогда, когда векторы
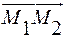 ,
, 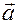 и
и 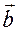 попарно коллинеарны.
попарно коллинеарны.
Задача 1. Определите взаимное расположение прямых
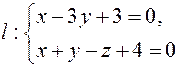 и
и 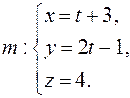
Задача 2. Напишите уравнения прямой, проходящей через точку 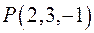 и пересекающей прямые:
и пересекающей прямые:
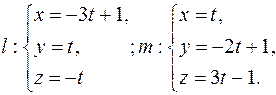
4.3. Взаимное расположение прямой и плоскости.
Зададим в аффинной системе координат прямую
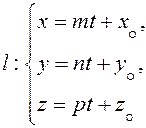 (20) и плоскость
(20) и плоскость 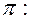
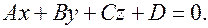 (21)
(21)
Будем искать общие точки прямой и плоскости. Для этого нужно решить систему уравнений (20) и (21):
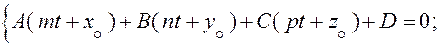
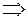
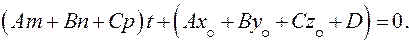
Обозначим: 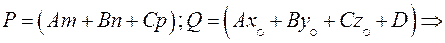
 (22)
(22)
Возможны следующие случаи.
1) Система (20),(21) имеет единственное решение 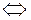
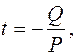
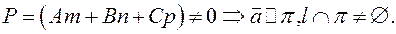
Прямая пересекает плоскость.
Решая систему (20),(21), найдем точку пересечения прямой и плоскости.
2) Система не имеет решений, если 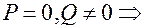
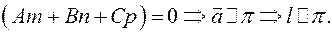
Причем, 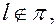 так как
так как 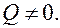 Прямая и плоскость параллельны.
Прямая и плоскость параллельны.
3)) Система (20),(21) имеет бесконечно много решений 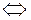
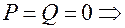
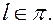 Прямая принадлежит плоскости.
Прямая принадлежит плоскости.
Задача. Определите взаимное расположение прямой 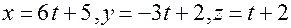 и плоскости
и плоскости 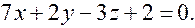
4.4.Прямая линия в системе координат 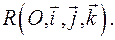 .
.
4.4.1. Угол прямой с плоскость.
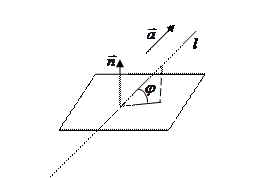 Опр. Углом прямой с плоскостью называется острый угол между этой прямой и её проекцией на плоскость.
Опр. Углом прямой с плоскостью называется острый угол между этой прямой и её проекцией на плоскость.
Зададим в системе координат 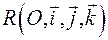
прямую 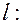
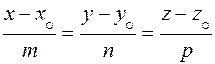 и плоскость
и плоскость 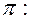
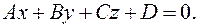
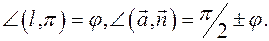
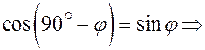
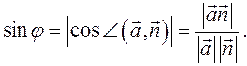 (22)
(22)
Условие параллельности прямой и плоскости:
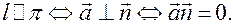
Условие перпендикулярности прямой и плоскости:
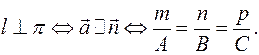
4.4.2. Угол между двумя прямыми.
Угол между двумя прямыми в пространстве определяется как угол между прямыми, параллельными данным и проходящим через одну точку. Его величину можно найти как угол между направляющими векторами прямых. Пусть заданы две прямые:
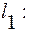
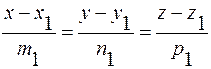 ;
;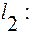
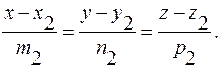
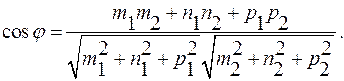
Задача 1. Найдите точку, симметричную точке 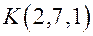 относительно плоскости
относительно плоскости 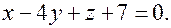
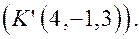
Задача 2. Найдите точку, симметричную точке 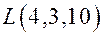 относительно прямой
относительно прямой 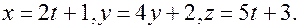
Задача 3. Найдите расстояние от точки 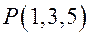 до прямой
до прямой
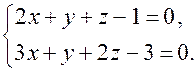
Задача 4. Найдите расстояние между диагональю куба с ребром 1 и не пересекающей её диагональю грани.
Задача 5. Составьте уравнения общего перпендикуляра двух скрещивающихся прямых
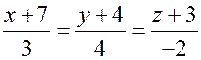 и
и 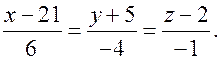
 2014-02-09
2014-02-09 523
523








