Цилиндрические поверхности

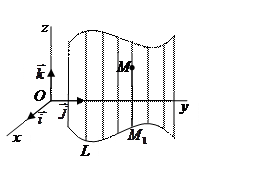
Зададим в пространстве некоторую линию

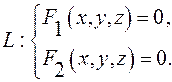(25)

Опр. Поверхность, образованная прямыми пространства, пересекающими некоторую линию 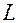и параллельными одной и той же прямой ,

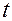пространства, называется цилиндрической поверхностью с направляющей 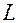и образующими, параллельными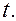

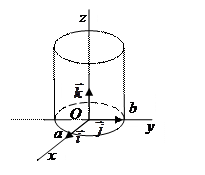
Пусть в дпск задана направляющая цилиндрической поверхности:

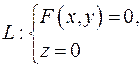
и направляющий вектор образующих 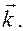Образующие цилиндрической поверхности параллельны оси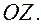

Составим уравнение цилиндрической поверхности. Пусть 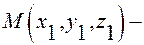её произвольная точка, прямая 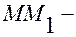её образующая, причем 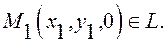Тогда выполняется равенство 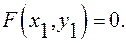И это справедливо для любой точки данной цилиндрической поверхности. Значит, уравнение этой поверхности

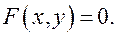
Аналогично получаются уравнения цилиндрических поверхностей с образующими, параллельными осям 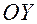и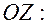

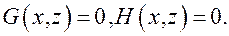
Вид цилиндрической поверхности определяется типом направляющей кривой.

Рассмотрим канонические уравнения цилиндрических поверхностей.

1) 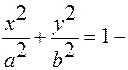эллиптический цилиндр;

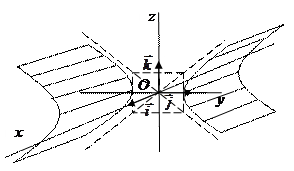
]2) 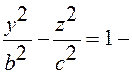гиперболический цилиндр;

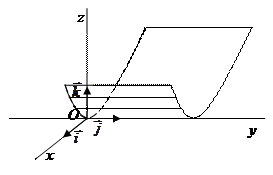3) 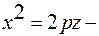параболический цилиндр;

4) 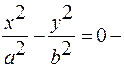цилиндр, распавшийся на пару пересекающихся по оси плоскостей;

5) 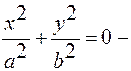пара мнимых пересекающихся по действительной оси плоскостей;

6) 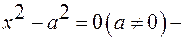пара параллельных плоскостей;

7) 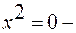две совпавшие плоскости;

8) 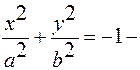мнимый эллиптический цилиндр.