Примеры задач, приводящих к дифференциальным уравнениям

Метод вариации произвольных постоянных (метод Лагранжа).

Пусть дано уравнение 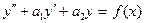, , 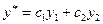f(x) – сложная функция (нет в таблице). Будем искать y в виде: 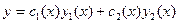. Вводим добавочное условие: 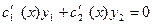, тогда 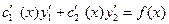. Составим систему

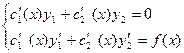, находим .

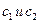Пример. 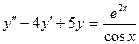- дифференциальное уравнение решается методом вариации произвольных постоянных.

Решение задач прикладного характера обычно состоит из трех частей:

1) составления дифференциального уравнения;

2) решение этого уравнения;

3) исследование решения.

При решении геометрических задач полезно пользоваться следующей последовательностью действий:

1) сделать чертеж и ввести обозначения. Например, f(x) – уравнение искомой линии и т.п.

2) отделить условия, имеющие место в произвольной точке искомого геометрического места, от условий, имеющих место лишь в отдельных фиксированных точках (т.е. выделить начальные условия).

3) выразить все упомянутые в задаче величины через x,y, 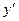, учитывая при этом геометрический смысл производной.

4) на основании условия задачи составить дифференциальное уравнение семейства искомых кривых.

5) найти общее решение дифференциального уравнения, а затем по начальным условиям найти конкретную интегральную кривую.

При решении физических задач полезно пользоваться следующей последовательностью действий:

1) Установить какому закону подчиняется процесс.

2) Решить, что выбрать за независимое переменное и что за искомую функцию.

3) Исходя из условия задачи, определить начальные условия.

4) Выразить все фигурирующие в задаче величины, используя при этом физический смысл производной как скорость изменения переменной в изучаемом процессе.

5) Исходя из условия задачи и на основании физического закона, которому подчиняется данный процесс, составить дифференциальное уравнение.

6) Найти общий интеграл дифференциального уравнения.

7) По начальным условиям найти частное решение.