2.
Свойства определённого интеграла
1. Постоянный множитель можно выносить за знак интеграла,
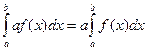 ,
,
где а - некоторое число.
2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
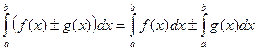 .
.
3. Если отрезок интегрирования разбит на части, то интеграл на всём отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых a, b, c.
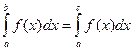 +
+ 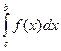 .
.
4. Если на отрезке 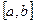 , где a < b, f(x) ≤ g(x), то и
, где a < b, f(x) ≤ g(x), то и
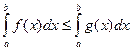 ,
,
т.е. обе части неравенства можно почленно интегрировать.
5. Теорема о среднем. Если функция у = f(х) непрерывна на отрезке 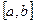 , (где a < b), то найдется такое значение ξє
, (где a < b), то найдется такое значение ξє 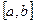 , что
, что
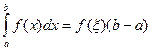 .
.
Если функция y = f(x) интегрируема на отрезке 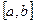 , то, очевидно, она интегрируема также на произвольном отрезке
, то, очевидно, она интегрируема также на произвольном отрезке 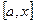 , вложенном в
, вложенном в 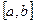 .
.
Положим по определению
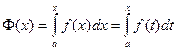 ,
,
где х є 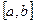 , а функция Ф(x) называется интегралом с переменным верxним пределом.
, а функция Ф(x) называется интегралом с переменным верxним пределом.
Свойства функции Ф(x)
Теорема 1. Если функция f(x) непрерывна на отрезке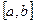 , то функция Ф (x) также непрерывна на
, то функция Ф (x) также непрерывна на 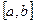 .
.
Теорема 2. Пусть функция f(x) непрерывна на отрезке 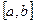 . Тогда в каждой точке х отрезка
. Тогда в каждой точке х отрезка 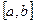 производная функции Ф (x) по переменному верxнему пределу равна подынтегральной функции f(x), т.е.
производная функции Ф (x) по переменному верxнему пределу равна подынтегральной функции f(x), т.е.
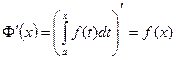 .
.
 2014-02-09
2014-02-09 621
621








