2014-02-09
415
Теорема 1. Пусть функция φ (t) имеет непрерывную производную на отрезке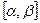
, а = φ (α), b = φ (β) и функция f(x) непрерывна в каждой точке х вида х = φ (t), где t є .
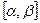Тогда справедливо следующее равенство
.
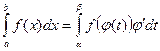Формула носит название формулы замены переменной в определённом интеграле.
Теорема 2. Пусть функции u = u (x) и v = v (x) имеют непрерывные производные на отрезке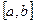 
. Тогда
,
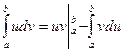где иv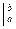
= u (b) v (b) - u (a) v (a).
Формула называется формулой интегрирования по частям для определённого интеграла.
Геометрическая интерпретация: определенный интеграл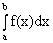 
представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y= f(x), прямыми x = a и x = b и отрезком оси Ox.
