Экономический смысл интеграла

Пусть функция z = f(t) описывает изменение производительности некоторого производства с течением времени. Найдем объем продукции u, произведенной за промежуток времени .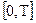

u = ,

т.е. если f(t) - производительность труда в момент t, то есть объем выпускаемой продукции за промежуток .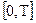

Сравнение данной задачи с задачей о площади криволинейной трапеции показывает, что величина и объема продукции, произведенной за промежуток времени 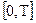, численно равна площади под графиком функции z = f(t), описывающей изменение производительности труда с течением времени, на промежутке 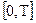или .

Достаточное условие существования определенного интеграла (интегрируемости функции). Теорема. Если функция у = f(х) непрерывна на отрезке 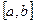, то она интегрируема на этом отрезке.