Замена переменной и формула интегрирования

3.

Формула Ньютона – Лейбница

Теорема. Пусть функция у = f(x) непрерывна на отрезке 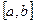и F(x) - любая первообразная для f(x) на 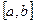. Тогда определённый интеграл от функции f(x) на 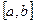равен приращению первообразной F(x) на этом отрезке, т.е.

.

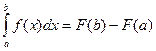Нахождение определенных интегралов с использованием формулы Ньютона - Лейбница осуществляется в два шага:

1. Используя технику нахождения неопределённого интеграла, находят некоторую первообразную F (x) для подынтегральной функции f(x);

2. Применяется собственно формула Ньютона - Лейбница - находится приращение первообразной, равное искомому интегралу. В связи с этим, введем обозначение для приращения первообразной, которое удобно использовать при записи решений. По определению положим

F (х)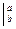= F(b) - F(a).

4.