Определение. Если существует и конечен предел 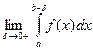 , гдеδ > 0, то он называется несобственным интегралом от функции y = f(x) на
, гдеδ > 0, то он называется несобственным интегралом от функции y = f(x) на 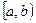 и обозначается
и обозначается
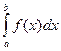 , т.е.
, т.е.
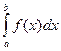 =
= 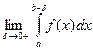 .
.
В этом случае данный несобственный интеграл называется сходящимся, в противном случае - расходящимся.
Аналогично вводится понятие несобственного интеграла от функции y = f(x) непрерывной, но неограниченной на 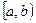 :
:
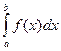 =
= 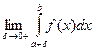 .
.
Пример. Вычислить интеграл 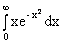 .
.
Решение. Подынтегральная функция определена и непрерывна при всех значениях х и, следовательно, имеет первообразную F(x)= 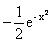 .
.
По определению имеем: 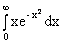 =
= 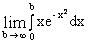 .
.
По формуле Ньютона-Лейбница,
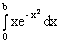 = F(b) - F(0) =
= F(b) - F(0) = 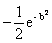 +
+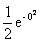 =
=  ;
;
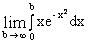 =
= 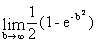 =
=  .
.
 2014-02-09
2014-02-09 510
510








