Для понимания третьего случая требуются элементарные знания про комплексные числа. Если материал позабылся, прочитайте урок Комплексные числа, в частности, параграф Извлечение корней из комплексных чисел.
Если характеристическое уравнение 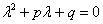 имеет сопряженные комплексные корни
имеет сопряженные комплексные корни 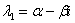 ,
, 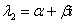 (дискриминант
(дискриминант 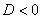 ), то общее решение однородного уравнения принимает вид:
), то общее решение однородного уравнения принимает вид:
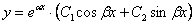 , где
, где 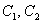 – константы.
– константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом: 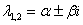
Если получаются чисто мнимые сопряженные комплексные корни: 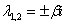 , то общее решение упрощается:
, то общее решение упрощается:
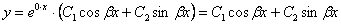
Пример 5
Решить однородное дифференциальное уравнение второго порядка
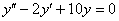
Решение: Составим и решим характеристическое уравнение:
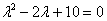
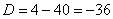
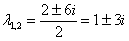 – получены сопряженные комплексные корни
– получены сопряженные комплексные корни
Ответ: общее решение: 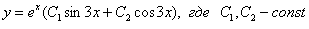
Пример 6
Решить однородное дифференциальное уравнение второго порядка
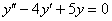
Полное решение и ответ в конце урока.
Иногда в заданиях требуется найти частное решение однородного ДУ второго порядка, удовлетворяющее заданным начальным условиям, то есть, решить задачу Коши. Алгоритм решения полностью сохраняется, но в конце задачи добавляется один пункт.
Пример 7
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям 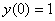 ,
, 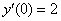
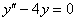
Решение: составим и решим характеристическое уравнение:
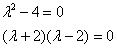
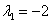 ,
, 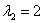
Получены два различных действительных корня, поэтому общее решение:
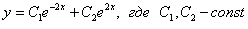
Теперь нужно найти частное решение, соответствующее заданным начальным условиям. Наша задача состоит в том, чтобы найти ТАКИЕ значения констант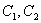 , чтобы выполнялись ОБА условия.
, чтобы выполнялись ОБА условия.
Алгоритм нахождения частного решения следующий:
Сначала используем начальное условие 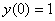 :
:
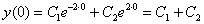
Согласно начальному условию, получаем первое уравнение: 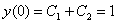 или просто
или просто 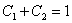
Далее берём наше общее решение 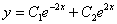 и находим производную:
и находим производную:
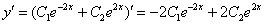
Используем второе начальное условие 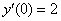 :
:
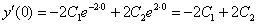
Согласно второму начальному условию, получаем второе уравнение: 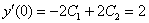 или просто
или просто 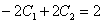
Составим и решим систему из двух найденных уравнений:
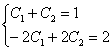
Допустимо использовать «школьный» метод решения, но в высшей математике чаще применяют метод почленного сложения/вычитания уравнений системы. В составленной системе удобно разделить второе уравнение на 2 и почленно сложить уравнения:
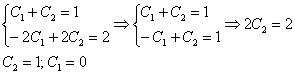
Всё, что осталось сделать – подставить найденные значения констант 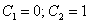 в общее решение
в общее решение 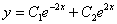 :
:
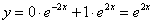
Ответ: частное решение: 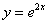
Проверка осуществляется по следующей схеме:
Сначала проверим, выполняется ли начальное условие 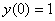 :
:
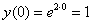 – начальное условие выполнено.
– начальное условие выполнено.
Находим первую производную от ответа:
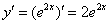
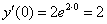 – второе начальное условие тоже выполнено.
– второе начальное условие тоже выполнено.
Находим вторую производную:
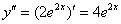
Подставим 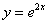 и
и 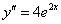 в левую часть исходного дифференциального уравнения
в левую часть исходного дифференциального уравнения 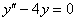 :
:
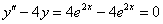 , что и требовалось проверить.
, что и требовалось проверить.
Такие образом, частное решение найдено верно.
Пример 8
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям 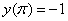 ,
, 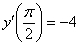 . Выполнить проверку.
. Выполнить проверку.
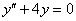
Это пример для самостоятельного решения, ответ в конце урока. Если не помните значения тригонометрических функций, используйте Тригонометрические таблицы.
Как видите, особых сложностей с однородными уравнениями нет, главное, правильно решить квадратное уравнение.
Иногда встречаются нестандартные однородные уравнения, например уравнение в виде 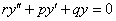 , где при второй производной есть некоторая константа
, где при второй производной есть некоторая константа 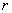 , отличная от единицы (и, естественно, отличная от нуля). Алгоритм решения ничуть не меняется, следует невозмутимо составить характеристическое уравнение и найти его корни. Если характеристическое уравнение
, отличная от единицы (и, естественно, отличная от нуля). Алгоритм решения ничуть не меняется, следует невозмутимо составить характеристическое уравнение и найти его корни. Если характеристическое уравнение 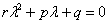 будет иметь два различных действительных корня, например:
будет иметь два различных действительных корня, например: 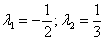 , то общее решение запишется по обычной схеме:
, то общее решение запишется по обычной схеме: 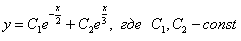 .
.
В ряде случаев из-за опечатки в условии могут получиться «нехорошие» корни, что-нибудь вроде 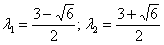 . Что делать, ответ придется записать так:
. Что делать, ответ придется записать так:
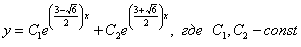
С «плохими» сопряженными комплексными корнями наподобие 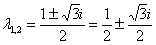 тоже никаких проблем, общее решение:
тоже никаких проблем, общее решение:
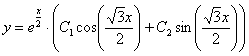
То есть, общее решение в любом случае существует. Потому-что любое квадратное уравнение имеет два корня.
 2014-02-09
2014-02-09 11219
11219
