Свойства сходящихся рядов

2.

1. Если ряд u₁ + u₂ +_….+ u_n + …сходится и имеет сумму S, то и ряд λu₁ + λu₂ + …. + λu_n + ….(полученный умножением данного ряда на число λ) также сходится и имеет сумму λS.

2. Если ряды u₁ + u₂ + …. + u_n + …. и v₁ + v₂ + …. + v_n + …. сходятся и их суммы соответственно равны S₁ и S₂, то и ряд (u₁ + v₁) + (u₂ + v₂) + (u_n + v_n)+_…. (представляющий сумму данных рядов) также сходится, и его сумма S₁ + S_2.

3. Если ряд сходится, то сходится и ряд, полученный из данного путём отбрасывания (или приписывания) конечного числа членов.

4. Для того чтобы ряд сходился, необходимо и достаточно, чтобы при n → ∞ остаток ряда стремился к нулю, т.е. чтобы 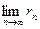= 0.