Основные понятия. Сходимость ряда

1.

Основные понятия. Сходимость и сумма числового ряда.

Т.3.1. Числовые ряды, 4ч.

Раздел 3. Числовые и степенные ряды

План

2.Свойства сходящихся рядов.

3.Признаки сходимости.

4.Знакочередующиеся ряды. Признак Лейбница.

Определение. Числовым рядом называется бесконечная последовательность чисел u₁, u₂, …, u_n …, соединенных знаком сложения:

u₁ + u₂ +….. + u_n + …= .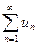

Числа u₁, u₂, …, u_n, …, называются членами ряда, а член u_n - общим или n-м членом ряда.

Ряд считается заданным, если известен его общий член u_n = f(n) (n = 1, 2,...), т.е. задана функция f(n) натурального аргумента.

Определение. Ряды называется сходящимся, если существует конечный предел последовательности его частичных сумм т.е.

.

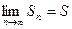Число S называется суммой ряда. В этом смысле можно записать

u₁ + u₂ +_…. + u_n + …= 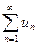= S.

Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.