Характеристическое уравнение имеет два кратных действительных корня

Если характеристическое уравнение 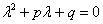имеет два кратных (совпавших) действительных корня 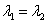(дискриминант 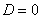), то общее решение однородного уравнения принимает вид:
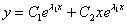, где 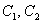– константы.
Вместо 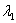в формуле можно было нарисовать 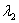, корни всё равно одинаковы.

Если оба корня равны нулю 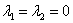, то общее решение опять же упрощается: 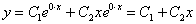. Кстати, является общим решением того самого примитивного уравнения 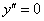, о котором упоминалось в начале урока. Почему? Составим характеристическое уравнение: – действительно, данное уравнение как раз и имеет совпавшие нулевые корни .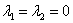

Пример 3

Решить дифференциальное уравнение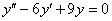

Решение: составим и решим характеристическое уравнение:

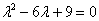
Здесь можно вычислить дискриминант, получить нуль и найти кратные корни. Но можно невозбранно применить известную школьную формулу сокращенного умножения:

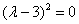
(конечно, формулу нужно увидеть, это приходит с опытом решения)

Получены два кратных действительных корня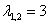

Ответ: общее решение: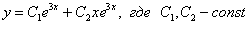

Пример 4

Найти общее решение дифференциального уравнения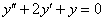

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Желающие могут потренироваться и выполнить проверку, но она здесь будет труднее.