Теорема (признак сравнения). Пусть даны два ряда с положительными членами:
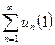 и
и 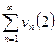 , причём члены первого рода не превосходят членов второго, т.е. при любом n un ≤ vn.
, причём члены первого рода не превосходят членов второго, т.е. при любом n un ≤ vn.
Тогда:
а) если сходится ряд 2, то сходится и ряд 1;
б) если расходится ряд 1, то расходится и ряд 2.
а) Пусть частичные суммы рядов 1 и 2 соответственно равны Sn и Sn. По условию ряд 2 сходится, следовательно, существует 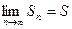 и Sn ≤ S, так как члены ряда 2 положительны. Рассмотрим последовательность частичных сумм Sn ряда 1. Эта последовательность является: возрастающей (так как с ростом n увеличивается сумма n положительных слагаемых) и ограниченной (так как Sn ≤ Sn в силу условия un ≤ vn, т.е. Sn ≤ Sn ≤ S).
и Sn ≤ S, так как члены ряда 2 положительны. Рассмотрим последовательность частичных сумм Sn ряда 1. Эта последовательность является: возрастающей (так как с ростом n увеличивается сумма n положительных слагаемых) и ограниченной (так как Sn ≤ Sn в силу условия un ≤ vn, т.е. Sn ≤ Sn ≤ S).
Следовательно, на основании признака существования предела последовательность Sn имеет предел, т.е. ряд 1 сходится.
б) Применим метод доказательства от противного. Предположим, что ряд 2 сходится. Тогда согласно первой части теоремы сходиться и ряд 1, что противоречит предположению, т.е. ряд 2 расходится.
Теорема (предельный признак сравнения). Если 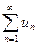 и
и 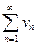 ряды с положительными членами и существует конечный предел отношения иx общиx членов
ряды с положительными членами и существует конечный предел отношения иx общиx членов
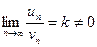 , то ряды одновременно сходятся, либо расходятся.
, то ряды одновременно сходятся, либо расходятся.
Так как 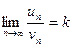 , то по определению предела числовой последовательности для любого ε > 0 существует такой номер N, что для всех n > N выполняется неравенство
, то по определению предела числовой последовательности для любого ε > 0 существует такой номер N, что для всех n > N выполняется неравенство
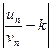 < ε или
< ε или 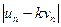 < ε vn, откуда (k - ε) vn < un < (k + ε) vn.
< ε vn, откуда (k - ε) vn < un < (k + ε) vn.
Теорема (признак Даламбера). Пусть для ряда 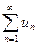 с положительными членами существует предел отношения (n + 1 )-го члена к n-му члену
с положительными членами существует предел отношения (n + 1 )-го члена к n-му члену 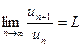 . Тогда, если L < 1, то ряд сходится; если L > 1, то ряд расходится; если L = 1, то вопрос о сходимости ряда остаётся нерешенным.
. Тогда, если L < 1, то ряд сходится; если L > 1, то ряд расходится; если L = 1, то вопрос о сходимости ряда остаётся нерешенным.
Замечание 1. Если 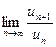 = ∞, то ряд расходится.
= ∞, то ряд расходится.
Замечание 2. Если 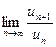 = L = 1, то, как отмечалось выше, признак Даламбера ответа о сходимости ряда не дает, и рекомендуется перейти к другим признакам сходимости.
= L = 1, то, как отмечалось выше, признак Даламбера ответа о сходимости ряда не дает, и рекомендуется перейти к другим признакам сходимости.
Теорема (интегральный признак сходимости). Пусть дан ряд 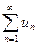 , члены которого положительны и не возрастают, т.е. u1 ≥ u2 ≥ ….. ≥ un ≥ ….., а функция f(x), определенная при x ≥ 1, непрерывная и невозрастающая и
, члены которого положительны и не возрастают, т.е. u1 ≥ u2 ≥ ….. ≥ un ≥ ….., а функция f(x), определенная при x ≥ 1, непрерывная и невозрастающая и
f (1) = u 1, f (2) = u 2, ….., f(n) = un , …..
Тогда для сходимости ряда 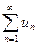 необходимо и достаточно, чтобы сходился несобственный интеграл
необходимо и достаточно, чтобы сходился несобственный интеграл 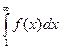 .
.
 2014-02-09
2014-02-09 1423
1423








