Ряды с членами произвольного знака

4.

Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны:

u₁ - u₂ + u₃ - u₄ +…+(-1) ^n-1u_n +…, где u_n >0.

Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине u₁ > u₂ >….> u_n > …. и предел его общего члена при n → ∞ равен нулю, т.е. 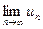= 0, то ряд сходится, а его сумма не превосходит первого члена: S ≤ u₁.

Рассмотрим последовательность частичныx сумм чётного числа членов при n = 2 m:

S _{2 m} = (u₁ - u₂) + (u₃ - u₄) +…+(u_2m-1 - u_2m).

Эта последовательность возрастающая (так как с ростом n = 2 m увеличивается число положительных слагаемых в скобках) и ограниченная (это видно из того, что S _{2 m} можно представить в виде

S _{2 m} = u₁ - (u₂ - u₃) + (u₄ - u₅)+ …+(u_2m-2 - u_2m-1) - u_2m,

откуда следует, что S _{2 m} < u₁. На основании признака существования предела последовательность S _{2 m} имеет предел .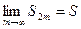

Попутно заметим, что переходя к пределу в неравенстве S_2m < u₁ при m → ∞, получим, что S ≤ u₁.

Теперь рассмотрим последовательность частичных сумм нечётного числа членов при n = 2 m + 1. Очевидно, что S _{2 m+1} = S _{2 m} + а _{2 m+1} ; поэтому, учитывая необходимый признак сходимости ряда, .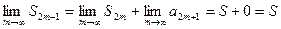

Итак, при любом n (четном или нечетном) 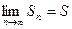, т.е. ряд сходится.

Замечание. В теореме Лейбница существенно не только условие 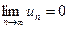, но и условие u₁ > u₂ >….> u_n > …. Так, например, для ряда

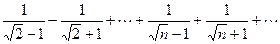
второе условие нарушено и, хотя 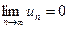, ряд расходится.

Следствие. Погрешность при приближённом вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющегося условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.

< ,

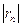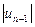где r_n – сумма,

u_n+1 - первый член.

Знакопеременные ряды. Пусть u₁ + u₂ +….+ u_n +…. знакопеременный ряд, в котором любой его член u_n может быть как положительным, так и отрицательным.

Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютныx величин членов данного ряда

,

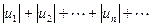сходится, то сходится и данный ряд.

Определение. Ряд называется абсолютно сходящимся, если сходятся как сам ряд, так и ряд, составленный из абсолютных величин его членов. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

С.Р. 1.Ряд геометрической прогрессии.

2. Остаток ряда и его свойства.