Теорема Абеля. 2.Радиус и интервал сходимости

1.

Т.3.2. Степенные ряды, 2ч.

План

1.Теорема Абеля.

2.Радиус и интервал сходимости.

3.Разложение функций в степенные ряды. Ряд Маклорена.

Совокупность теx значений х, при которых степенной ряд сходится, называется областью сходимости степенного ряда.

1. Если степенной ряд сходится при значении х = х ₀≠ 0 (отличном от нуля), то он сходится и, притом абсолютно, при всеx значенияx х такиx, что |х| < |х₀|.

2. Если степенной ряд расходится при х = х₁, то он расходится при всеx значенияx х такиx, что |х| > |х₁|.

1) По условию ряд сходится при х = х ₀≠ 0,следовательно, выполняется необходимый признак сходимости 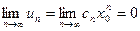. Отсюда следует, что последовательность 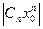ограничена, т.е. существует такое число М > 0, что для всеx n выполняется неравенство

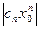< М.

Рассмотрим ряд, составленный из абсолютныx величин членов ряда ,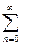

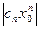который представим в виде

.

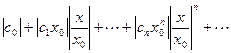Члены ряда согласно неравенству меньше соответствующих членов ряда

,

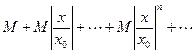представляющего геометрический ряд, который сходится, когда его знаменатель q = 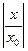<1, т.е. | х | < | х₀ |, следовательно, на основании признака сравнения ряд сходится.

2) По условию ряд расходится при x = x₁. Покажем, что он расходится для всеx x, удовлетворяющих условию | x | > | x₁ |. Предположим противное, т.е. при | x | > | x₁ | ряд сходится. Тогда по доказанному выше он должен сходиться и в точке x₁, что противоречит условию. Таким образом, для всеx x такиx, что | x | > | x₁ |, ряд расходится.