Определение. Открытым шаром радиуса 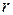 с центром в точке
с центром в точке 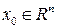 называется множество
называется множество
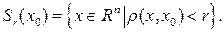
Определение предела (по Коши) функции 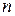 переменных полностью повторяет определение предела для функции одной переменной.
переменных полностью повторяет определение предела для функции одной переменной.
Определение. Пусть функция 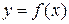 определена в шаре
определена в шаре 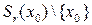 , где
, где 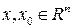 и
и 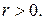 Число
Число 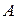 называется пределом функции
называется пределом функции 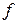 в точке
в точке 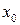 и при этом пишут
и при этом пишут 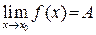 (или
(или 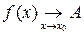 ), если
), если 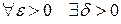 такое, что
такое, что 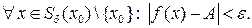
Точно также как для функции одной переменной доказываются следующие свойства предела:
1) Предел единственен;
2) Предел суммы, разности или произведения функций в точке 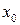 равен сумме, разности или произведению пределов при условии, что они существуют.
равен сумме, разности или произведению пределов при условии, что они существуют.
3) Предел отношения двух функции в точке 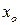 равен отношению пределов, при условии, что предел знаменателя не равен
равен отношению пределов, при условии, что предел знаменателя не равен 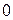 .
.
Определение. Пусть функция 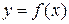 определена в шаре
определена в шаре 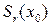 , где
, где 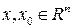 и
и 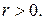 Функция
Функция
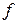 называется непрерывной в точке
называется непрерывной в точке 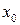 , если
, если
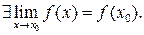
В противном случае функция 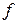 называется разрывной в точке
называется разрывной в точке 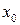 . Функция
. Функция 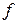 называется непрерывной на множестве
называется непрерывной на множестве 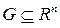 , если она непрерывна в каждой точке множества
, если она непрерывна в каждой точке множества 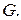
Из свойств предела следуют следующие свойства непрерывных функций:
1)Если функции 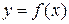 и
и 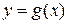 , где
, где 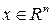 непрерывны в точке
непрерывны в точке 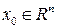 , то в точке
, то в точке 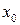 непрерывны функции
непрерывны функции 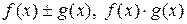 , а также
, а также 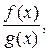 если
если 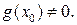
2) Если функция 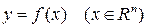 непрерывна в точке
непрерывна в точке 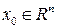 , а функция
, а функция 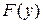 непрерывна в точке
непрерывна в точке 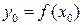 , то сложная функция
, то сложная функция 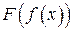 непрерывна в точке
непрерывна в точке 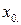
При изучении свойств функций многих переменных удобно исследовать линии уровня и графики функций.
Определение. Пусть дана функция 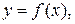 где
где 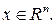 Линией уровня, соответствующей значению
Линией уровня, соответствующей значению 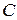 , называется множество
, называется множество
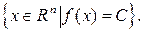
Замечание. Линия уровня функции двух переменных 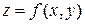 представляет собой множество точек плоскости, удовлетворяющие равенству
представляет собой множество точек плоскости, удовлетворяющие равенству
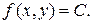
Пример. Линиями уровня функции 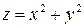 при
при 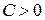 являются концентрические окружности
являются концентрические окружности
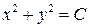 .
.
Определение. Графиком функции двух переменных 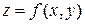 называется множество точек пространства
называется множество точек пространства
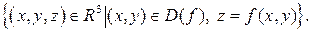
 2014-02-17
2014-02-17 452
452







