В качестве одного из приложений дифференциального исчисления функций многих переменных рассмотрим задачу о касательной плоскости к поверхности.
Теорема 1. Пусть поверхность 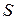 является графиком функции
является графиком функции 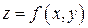 и функция
и функция 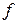 имеет непрерывные частные производные в
имеет непрерывные частные производные в 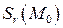 , где
, где 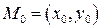 и
и 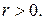 Тогда в точке
Тогда в точке 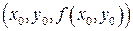 существует касательная плоскость к поверхности
существует касательная плоскость к поверхности 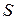 , которая задается уравнением:
, которая задается уравнением:
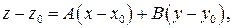
где 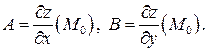
Теорема 2. Пусть поверхность 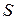 задана уравнением
задана уравнением 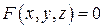 и точка
и точка 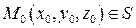 , то есть
, то есть 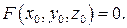 Пусть также
Пусть также 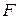 имеет непрерывные частные производные в
имеет непрерывные частные производные в 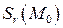 , где
, где 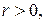 и
и 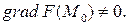 Тогда в точке
Тогда в точке 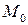 существует касательная плоскость к поверхности
существует касательная плоскость к поверхности 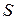 , которая задается уравнением
, которая задается уравнением
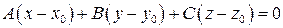 , где
, где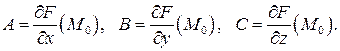
Пример. Найти уравнение касательной плоскости к поверхности
 в точке
в точке 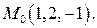
Решение.
Вычислим частные производные в точке 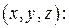
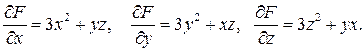
Тогда в соответствии с теоремой 2 находим
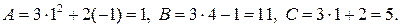
Уравнение касательной плоскости имеет вид
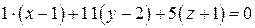 или
или 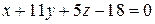 .
.
 2014-02-17
2014-02-17 1689
1689
