Градиент скалярного поля

Пусть на множестве 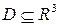задана функция 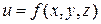и в каждой точке множества 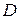существуют все частные производные функции .

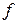Определение. Градиентом функции 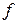в точке 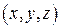называют вектор, координатами которого являются значения частных производных функции 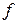в этой точке. Этот вектор обозначается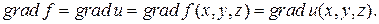

Таким образом,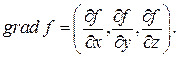

Говорят, что на множестве 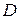определено поле градиента, если в каждой точке 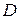определен вектор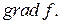

Замечание. Градиентом функции двух переменных 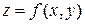называется вектор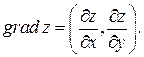

Отметим без доказательства важное свойство градиента:

Градиент функци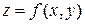и (или 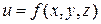) в точке 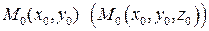, то есть вектор 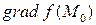, перпендикулярен линии уровня (поверхности уровня), проходящей через 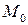, и направлен в сторону максимального увеличения функции.