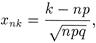Теоремы Муавра-Лапласа

Рассмотрим последовательность испытаний Бернулли B ₁,..., B_n,... с вероятностью успеха р. Определим

и пусть С и e положительные числа.

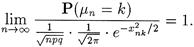Теорема 1 (локальная теорема Муавра-Лапласа). Пусть имеется последовательность испытаний Бернулли с вероятностью успеха р, тогда для всех k, таких, что ô x_nk ô£ C × n ^{(1/6)- e} имеет место

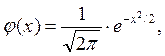Вводя функцию

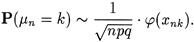которую называют функцией Гаусса, переформулируем утверждение теоремы, т.е. справедливо следующее приближенное равенство

Здесь и в дальнейшем знак «~» будет означать асимптотическую эквивалентность, определенную ниже.

Определение. Пусть a_n и b_n последовательности положительных чисел таких, что при п ®¥ имеет место a_n ® 0 и b_n ® 0. Будем говорить, что последовательности a_n и b_n асимптотически эквивалентны, если lim _{n ®¥} a_n/b_n = 1, и это обозначается как a_n ~ b_n.

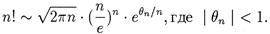Теорему доказывать не будем (см. например [3]), отметив лишь, что при доказательстве наряду с другими вспомогательными утверждениями используется формула Стирлинга:

Пример 1. Оператор обслуживает 25 однотипных приборов. Вероятность того, что прибор потребует к себе внимания оператора в течение промежутка времени Т равна 0,4. Найдем вероятность того, что за время Т три прибора потребуют к себе внимания оператора. Применим локальную теорему Муавра-Лапласа

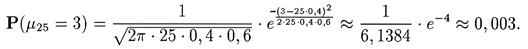поскольку р = 0,4 и пр == 10.

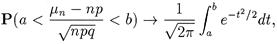Теорема 2 (интегральная теорема Муавра-Лапласа). Пусть имеется последовательность испытаний Бернулли с вероятностью успеха р. тогда при п 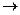¥ справедливо

где а и b—некоторые вещественные числа.

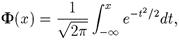Учитывая, что функция распределения стандартного нормального закона

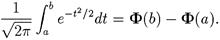в правой части (2.1) получаем

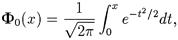Доказательство и этой теоремы здесь приводить не будем (см. в [3]), отметим лишь, что эта теорема является следствием более общей центральной предельной теоремы, которую мы рассмотрим позже. Заметим также, что иногда функция Ф (x) заменяется функцией Лапласа вида

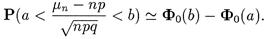Эта функция является нечетной, т.е. 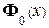= - 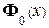, и кроме Ф (x) = 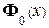+ 1/2. Тогда утверждение теоремы имеет вид:

Пример 2. Вероятность выпуска бракованной детали р = 0,02. Найдем вероятность того, что в партии из 200 деталей бракованных будет не больше 5. Здесь п = 200, р = 0,02, q = 0, 98, следовательно пр =- 200 • 0, 02 = 4, npq» 4 и по условию 0 £ m₅ £ 5. Найдем а и b:

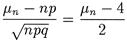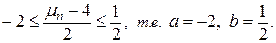и учитывая условия задачи

Тогда, по теореме 2 находим

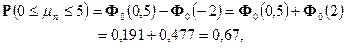
где значения 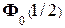= 0,191 и 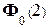= 0,477 найдены из таблицы значений функции 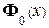(см. Таблицу 1 Приложения).