1. Математическое ожидание постоянной равно этой постоянной, т.е. если с – постоянная, то MX = c.
Доказательство. Постоянную можно рассматривать как случайную величину, принимающую значения с с постоянной вероятностью p = 1, тогда по формуле (1) имеем
MX = 1 c = c.
2. M (сX) = сMX.
Это свойство следует из теорем 1, 2.
3. Если определены MX и MY, то
M (X + Y) = MX + MY,
причем это свойство верно как для зависимых, так и для независимых случайных величин.
Доказательство. Докажем это свойство для конечных дискретных случайных величин. В соответствии с определением суммы случайных величин X + Y представляют случайную величину, которая принимает значения xi + yj с вероятностью
pij = P [(X = xi), (Y = yj)],
поэтому
M (X + Y) = 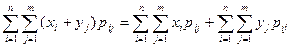 .
.
Так как в первой двойной сумме xi не зависит от индекса j, по которому ведется суммирование по второй сумме, и аналогично, во второй двойной сумме yj не зависит от индекса i, то
M (X + Y)=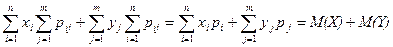
Мы воспользовались свойством, что  (см. лекцию 8)
(см. лекцию 8)
4. Если Х и Y независимы, то M (X Y) = MX MY
Доказательство.
M (X,Y) =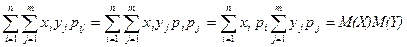
Пример 1. Найдем математическое ожидание нормальной случайной величины Х ~ N (a, s).
|
|
|
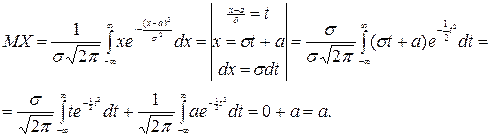
Таким образом, МХ = а.
Пример 2. Найдем математическое ожидание числа успехов в n испытаниях Бернулли.
Пусть Х имеет биномиальное распределение: 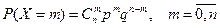 .
.
Обозначим через Xi – случайную величину, равную числу успехов в i -м испытании, тогда
Р (Хi = 0) = q, Р (Хi = 1) = p, MXi = 0 q + 1 p = p, но
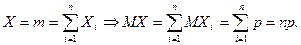
Таким образом, МХ = np.
ЛЕКЦИЯ 14. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН (продолжение)
Пусть Z = (X,Y) – двумерная случайная величина. Рассмотрим, как найти условное среднее случайной величины Z при условии, что Y = y. Предположим, что Z – дискретная случайная величина, pij = P (X = xi, Y = yj), 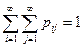 . На предыдущих лекциях (лекция 8) нами было показано, что
. На предыдущих лекциях (лекция 8) нами было показано, что
 ;
; 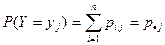 ,
,
и что условные вероятности
 ;
; 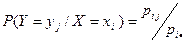
удовлетворяют условиям
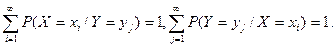
Поэтому при фиксированных уj и хi, вероятности P (X = xi/Y = yj), P (Y = yj / X = xi) можно рассматривать как условные распределения случайных величин Х (при условии, что Y = yj) и Y (при условии, что Х = хi). Тогда
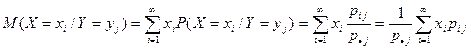
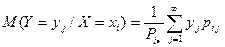
Предположим, что Z – непрерывная двумерная случайная величина, pz(Х,Y) – плотность Z; px(x) – плотность X; p y(y) – плотность Y. Тогда условную плотность распределения Х при условии, что Y = y, определим
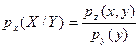 ,
,
а условную плотность распределения Y при условии, что Х = х, определим
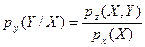 .
.
Найдем условное математическое ожидание Х при условии, что Y = y в соответствии с формулой (2) предыдущей лекции
M (X/y) = M (X / Y = y)=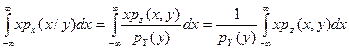
Аналогично,
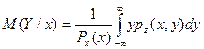 .
.
Функция fx (y) = М (Х / у) каждому у ставит в соответствие условное математическое ожидание Х при условии, что Y = y, т.е. она отражает зависимость от у условного среднего Х. Функция fx (y) = М (Х / у) называется функцией регрессии Х на У.
Аналогично, функция fу (х) = М (Y/x) называется функцией регрессии Y на Х.
|
|
|
Найдем математическое ожидание от математического ожидания М(X/у). Ограничимся рассмотрением дискретных случайных величин.
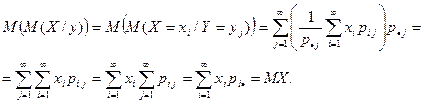
Таким образом, M (M (X / y)) = MX и называется формулой полного математического ожидания.
 2014-02-18
2014-02-18 1630
1630
