Выше мы рассматривали только монохроматические волны, имеющие одну частоту и длину волны. Значительно более общим является случай, когда волны существуют в виде набора или группы частных гармоник. Например, белый свет имеет сплошной спектр, занимающий участок видимого диапазона примерно от 3000Å в голубой области до 7000Å в красной области. Анализ поведения таких пакетов приводит к понятию групповой скорости, упомянутому в начале главы.
Рассмотрим пакет из двух компонент с одинаковой амплитудой, но с разными частотами 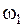 и
и 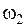 , различающимися на малую величину. Их отдельные смещения описываются формулами
, различающимися на малую величину. Их отдельные смещения описываются формулами
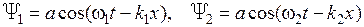 . (7.24)
. (7.24)
Складывая Ψ1 и Ψ2, получаем выражение
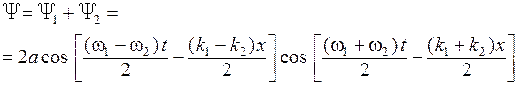 , (7.25)
, (7.25)
описывающее волну с частотой 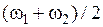 , которая очень близка к частоте любой из двух компонент. Амплитуда волны, имеющая максимальное значение 2 a, модулирована в пространстве и времени очень медленно меняющейся огибающей с частотой
, которая очень близка к частоте любой из двух компонент. Амплитуда волны, имеющая максимальное значение 2 a, модулирована в пространстве и времени очень медленно меняющейся огибающей с частотой 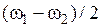 и с волновым числом
и с волновым числом 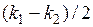 . Поведение такой волны представлено на рис. 7.5. Скорость новой волны равна
. Поведение такой волны представлено на рис. 7.5. Скорость новой волны равна
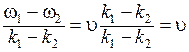 , (7.26)
, (7.26)
где через u обозначена фазовая скорость: 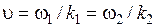 . Следовательно, частотные гармоники и их сумма, т. е. пакет, будут распространяться с одинаковой скоростью, причем профиль пакета, изображенного на рис. 7.5, не изменяется.
. Следовательно, частотные гармоники и их сумма, т. е. пакет, будут распространяться с одинаковой скоростью, причем профиль пакета, изображенного на рис. 7.5, не изменяется.
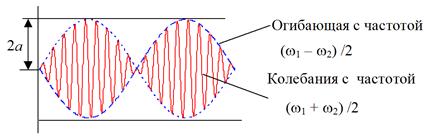
Рис. 7.5.
Теперь предположим, что две гармоники, рассмотренные в предыдущем разделе, имеют разные фазовые скорости и 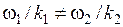 . Скорость максимума амплитуды пакета, т. е. групповая скорость,
. Скорость максимума амплитуды пакета, т. е. групповая скорость,
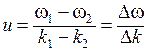 (7.27)
(7.27)
теперь отлична от каждой из этих скоростей. Вид суперпозиции двух волн уже не будет сохраняться неизменным, и профиль пакета будет изменяться со временем.
Среда, в которой фазовая скорость зависит от частоты (отношение w/ k не является постоянным), называется диспергирующей средой. Зависимость wот k выражается дисперсионной формулой. Если пакет состоит из гармоник с почти одинаковыми частотами, то исходное выражение для групповой скорости записывается следующим образом:
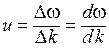 . (7.28)
. (7.28)
Групповая скорость есть скорость максимальной амплитуды пакета, а потому эта скорость, с которой переносится энергия пакета.
Поскольку w=ku, где u - фазовая скорость, групповая скорость равна
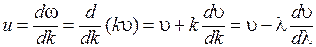 , (7.29)
, (7.29)
где 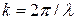 .
.
Обычно производная 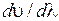 положительна, так что u< u. Это случай нормальной дисперсии. Но возможна аномальная дисперсия – когда производная
положительна, так что u< u. Это случай нормальной дисперсии. Но возможна аномальная дисперсия – когда производная 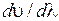 отрицательна и u >u. В фиксированный момент времени волновой пакет дает волновую картину, показанную на рис. 7.6.
отрицательна и u >u. В фиксированный момент времени волновой пакет дает волновую картину, показанную на рис. 7.6.
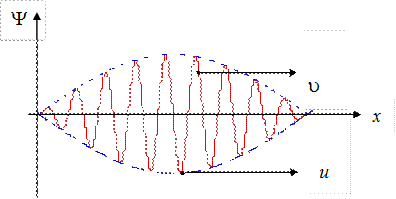
Рис. 7.6.
При рассмотрении электромагнитных волн мы увидим, что для таких волн электрический проводник обладает аномальной дисперсией, а диэлектрик – нормальной дисперсией всюду, кроме небольших областей около собственных резонансных частот атомов, образующих диэлектрик.
Контрольные вопросы
1. Возможно ли образование сходящейся сферической волны?
2. Что понимается под уравнением волны и волновым уравнением?
3. Каковы должны быть свойства среды, чтобы для механических волн в этой среде выполнялся принцип суперпозиции?
4. Каков физический смысл групповой скорости?
5. От чего зависит фазовая скорость волн в упругой среде?
Задачи
1. При отражении от преграды в образующихся стоячих волнах отношение амплитуды в пучности к амплитуде в узле равно d. Какая часть энергии уходит за преграду?
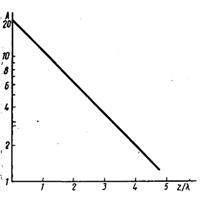
2. Волна распространяется в среде с затуханием. На графике по оси абсцисс отложено расстояние от источника колебаний, причем это расстояние выражено в длинах волн. По оси ординат отложен десятичный логарифм амплитуды. Написать на основании этого графика формулу, представляющую зависимость амплитуды от расстояния.
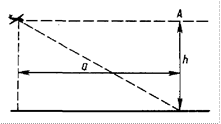
3. Самолет летит над землёй на высоте h со сверхзвуковой скоростью. На каком наименьшем расстоянии a (по горизонтали) от стоящего на земле наблюдателя должна находится такая точка, из которой звук самолёта доходит до наблюдателя раньше, чем из точки A над его головой?
4. Складываются два одинаково направленных колебания: 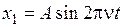 ,
, 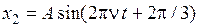 . Сравнить амплитуду А с амплитудой результирующего колебания.
. Сравнить амплитуду А с амплитудой результирующего колебания.
 2014-02-24
2014-02-24 1602
1602
