1°..
ЛОГАРИФМИЧЕСКИМИ И СТЕПЕННЫМИ ФУНКЦИЯМИ
ПРЕДЕЛЫ, СВЯЗАННЫЕ С ПОКАЗАТЕЛЬНЫМИ,
Из второго замечательного предела следует, что:
Используя непрерывность логарифмической функции, меняем местами знак предела и знак функции.
2°. 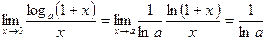 . Здесь достаточно вспомнить связь между логарифмами с различными основаниями.
. Здесь достаточно вспомнить связь между логарифмами с различными основаниями.
3°. 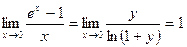 . Для перехода от первого предела ко второму выполнена замена переменных в предельном переходе:
. Для перехода от первого предела ко второму выполнена замена переменных в предельном переходе: 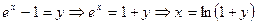 .
.
4°. 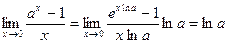 . Осуществлен переход к натуральному основанию.
. Осуществлен переход к натуральному основанию.
5°. 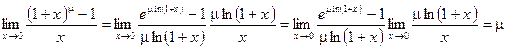 .
.
Использована теорема о пределе произведения двух функций, имеющих предел.
Рассматривается степенно-показательное выражение:
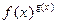 и при этом
и при этом 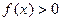 .
.
 2014-02-24
2014-02-24 691
691








