Напоминаем: Если 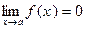 то функция f (x) называется бесконечно малой величиной и обозначается
то функция f (x) называется бесконечно малой величиной и обозначается 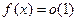 .
.
Если 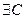 такое, что при
такое, что при 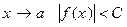 , то функция
, то функция 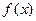 называется ограниченной и обозначается
называется ограниченной и обозначается 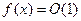 .
.
Def.
1) f (x) = o (g (x)) при x ® a Û $ h (x) f (x)= h (x) g (x) и h (x)= o (1).
Читается: f (x)есть величина бесконечно малая по сравнению с g (x).
2) f (x) = O (g (x)) при x ® a Û $ h (x) f (x)= h (x) g (x) и h (x)= O (1).
Читается: f (x)есть величина ограниченная по сравнению с g (x).
3) f (x)~ g (x) при x ® a Û $ h (x) f (x)= h (x) g (x) и h (x)=1+ o (1).
Читается: величины f (x)и g (x) эквивалентны.
4) f (x)≍ g (x) при x ® a Û $ h (x) f (x)= h (x) g (x);
h (x)= O (1) и отделена от нуля.
Читается: величины f (x)и g (x) одного порядка.
Немного другие формы записи тех же определений.
Def.
1) o (f (x)) =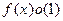 Û
Û 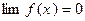 ,
,
2) O (f (x)) =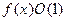 ,
,
3) f (x)~ g (x) Û  ,
,
4) f (x)≍ g (x) Û 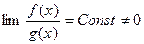 .
.
При этом:
1˚ f (x) = o (g (x)) Þ f (x) = O (g (x));
2˚. f (x)~ g (x) Þ f (x)≍ g (x);
3˚ f (x)~ g (x) Þ f (x) = O (g (x));
4˚ f (x)≍ g (x) Û f (x) = O (g (x)) Ù g (x) = O (f (x)).
Все эти соотношения транзитивны:
1˚ f (x) = o (g (x))Ù g (x) = o (h (x))Þ f (x) = o (h (x));
2˚ f (x) = O (g (x))Ù g (x) = O (h (x))Þ f (x) = O (h (x));
3˚ f (x)~ g (x)Ù g (x)~ h (x)Þ f (x)~ h (x);
4˚ f (x)≍ g (x)Ù g (x)≍ h (x)Þ f (x)≍ h (x).
Отношения эквивалентности, ограниченности и однопорядковости рефлексивны, т.е.
1˚ f (x)~ f (x);2˚ f (x) = O (f (x)); 3˚ f (x)≍ f (x).
Отношение пренебрежимости не рефлексивно и не симметрично
1˚ f (x)≠ o (f (x)); 2˚ f (x) = o (g (x)) Þ g (x)≠ o (f (x)).
Отношение эквивалентности и однопорядковости симметрично
1˚ f (x)~ g (x) Þ g (x)~ f (x);
2˚ f (x)≍ g (x) Þ g (x)≍ f (x).
Отношение относительной ограниченности антисимметрично
f (x) = O (g (x)) Ù g (x) = O (f (x)) Þ f (x)≍ g (x).
В произведениях и в суперпозициях о -символов получаем, как результат, наименьшее о, а в суммах наибольшее О.
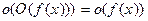 ;
; 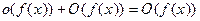 .
.
Все отношения (кроме эквивалентности) не чувствительны к знаку входящих функций.
Def. Если функция f (x)может быть представлена в виде суммы двух слагаемых, причем второе есть величина бесконечно малая по сравнению с первым 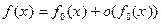 , то первое слагаемое f 0(x) называется главным членом функции f (x).
, то первое слагаемое f 0(x) называется главным членом функции f (x).
Т˚. Две величины эквивалентны тогда и только тогда, когда разность между ними есть величина бесконечно малая по сравнению с любой из них.
Δ f (x)~ g (x) Û  Û
Û 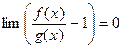 Û
Û 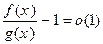 Û
Û 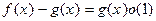 Û
Û 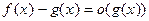 .
.
Аналогично получаем, что 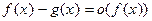 . ▲
. ▲
Т˚. Если эквивалентные величины имеют пределы, то эти пределы равны. Δ ▲.
Т˚. Главный член произведения равен произведению главных членов.
Δ Пусть 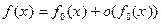 и
и 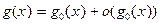 т.е.
т.е. 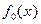 и
и 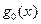 являются главными членами функций
являются главными членами функций 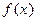 и
и 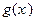 соответственно. Тогда:
соответственно. Тогда:
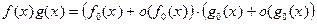 =
=
=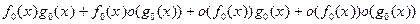 =
=
=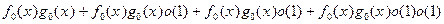 =
=
=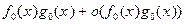 .
.
Следовательно, 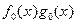 есть главный член для произведения
есть главный член для произведения 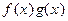 . ▲
. ▲
Замечание: Обращаем внимание на то, что главный член суммы (разности), вообще говоря, не равен сумме (разности) главных членов.
На (+∞) показательная функция с основанием больше 1 (меньше 1) растет (убывает) быстрее любой степени, а логарифмическая функция возрастает медленнее любой степени:
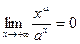 ;
; 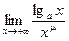 .
.
 2014-02-24
2014-02-24 494
494








