Применение производных к исследованию свойств функций

Неравенство Минковского.

Неравенство Коши – Буняковского – Шварца.

Из неравенства Гёльдера следует, что

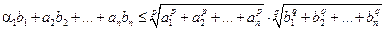
или, что тоже: 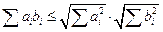(для ).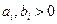

В общем случае: .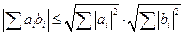

.

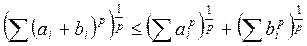и построению их графиков. Общая схема.

1. совпадение или подобие с графиками известных функций.

1°. Область определения функции, четность, нечетность, периодичность.

Def. Множество значений аргумента, для которых определено значение функции называется областью определения функции и обозначается .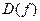

Def. Функция 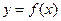называется четной, если .

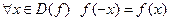График четной функции симметричен относительно оси абсцисс.

Def. Функция 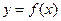называется нечетной, если .

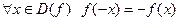График нечетной функции симметричен относительно начала координат.

Def. Функция 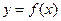называется периодической, если существует 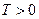, такое что

.

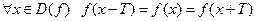2°. Поведение функции на границах области определения. Асимптоты.

Исследование включает в себя определение характера точек разрыва функции и ее поведения на бесконечности. Для этого находятся соответствующие пределы.

Правило 1. Если при 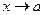(т.е. к конечному значению) функция 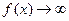, то функция имеет вертикальную асимптоту ().

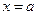Правило 2. Если при 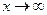функция 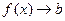(т.е. к конечному значению), то функция имеет горизонтальную асимптоту ().

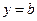Правило 3. Если при 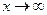функция 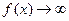, то возможно, что функция имеет наклонную асимптоту ().

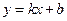∆ Для получения необходимых и достаточных условий существования наклонных асимптот рассмотрим следующий предел, который для асимптоты 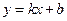, по определению, равен нулю.

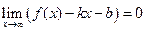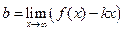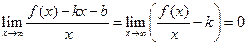Þ .

Þ .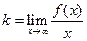

Итак, для того, чтобы функция 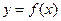имела наклонную асимптоту вида ,

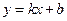необходимо и достаточно чтобы существовали и были конечны следующие два предела:

, .

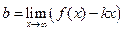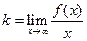Аналогично: необходимым и достаточным условием существования асимптот вида 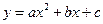является существование и конечность следующих пределов:

, , .

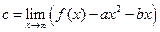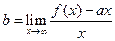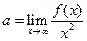Не составляет большого труда получить необходимые и достаточные условия существования асимптот более сложного вида, скажем вида 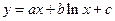или 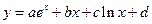и др. ▲.

3°. Пересечение графика функции с осями координат, промежутки знакопостоянства функции.

Вычислив значение функции в точке 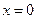получим координаты точки пересечения графика функции с осью ординат.

Решая уравнение 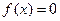найдем координаты точек пересечения графика функции с осью абсцисс. Зная эти точки и точки, которые не входят в область определения функции, с помощью метода интервалов, находим промежутки знакопостоянства функции.

4°. Построениепервого эскизаграфика.

5°. Нахождение производной 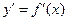функции.

6°. Нахождение критических точек функции, т.е. точек в которых производная функции не существует или равна нулю. Эти точки являются точками «подозрительными» на экстремум, если, конечно, они принадлежат области определения.

7°. Зная критические точки функции, с помощью метода интервалов, устанавливаем промежутки монотонности функции. Функция возрастает на промежутках, на которых 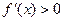и убывает на промежутках, на которых .

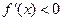8°. Для критических точек проверяем достаточные условия экстремума функции.

Если при возрастании аргумента производная функции меняет знак с «+» на «–», то в данной точке функция имеет максимум, если же при возрастании аргумента производная функции меняет знак с «–» на «+», то в данной точке функция имеет минимум. Если исследование поведения знака производной в окрестности точки вызывает значительные технические трудности, проверка достаточных условий экстремума функции может быть отложено до нахождения второй производной.

9°. Нахождение второй производной 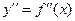функции.

10°. Проверка достаточных условий экстремума функции. Если в критической точке вторая производная функции положительна то функция в этой точке имеет минимум. Если в критической точке вторая производная функции отрицательна то функция в этой точке имеет максимум.

11°. Если на промежутке вторая производная функции положительна то функция вогнута (выпукла вниз). Если на промежутке вторая производная функции отрицательна то функция выпукла (выпукла вверх).

12°. Если в некоторой точкевтораяпроизводная функции равна нулю или не существует, а в окрестности этой точки меняет знак, то в этой точке функция имеет точку перегиба.

13°. Контрольные точки графика иокончательный эскиз графика функции.

NB: Схема – не догма! Схема – руководство к действию!