Примеры построения графиков функций

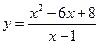1°. . 2°. .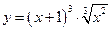

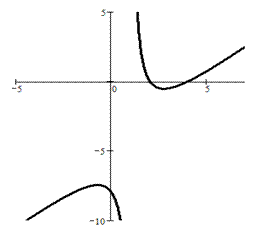
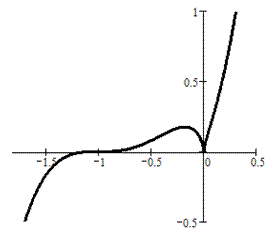
3°. Построить график функции заданной неявно: 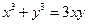. (Декартов лист).

Введем параметризацию: 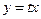. Подставляя в уравнение, получим: .

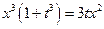И, наконец, задаем функцию параметрически: , ; .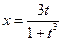

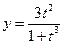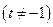Рассмотрим поведение функци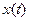й и 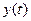на границах области определения, т.е. при t стремящихся к единице справа и слева, а также при t стремящихся бесконечности.

; .

; .

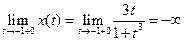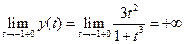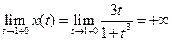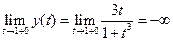Полученные соотношения говорят о том, что функция может иметь наклонные асимптоты. Найдем наклонные асимптоты, если они есть.

, .

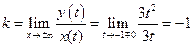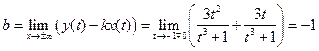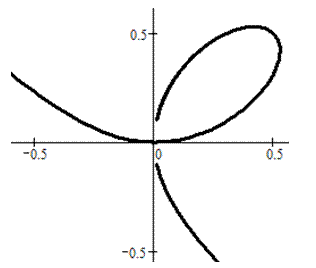Эти пределы одинаковы 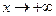при и при 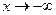, т.е. 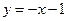является асимптотой функции при .

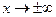При t = 0 функци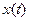и и 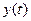обращаются в ноль (точка пересечения с осями). При этом график функции подходит к началу координат из первой и второй четверти.

Кроме того: , .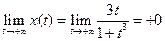

, .

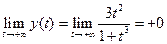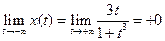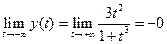Т.е. график функции подходит к началу координат из первой и четвертой четверти, но начала координат не достигает.

Для исследования динамических характеристик функции найдем производные функций и .

,

.

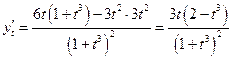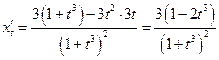Найдем нули найденных производных: 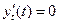при 1). 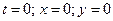и 2). .

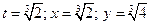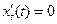при .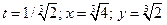

И, наконец 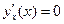при 1). 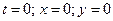и 2). 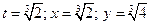.Изменение знака производной показывает что, в случае 1) функция 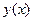имеет минимум, а в случае 2) функция имеет максимум и в этих точках касательная к графику функции горизонтальна.

При 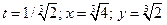производная 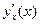не существует, а 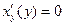и функция 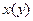в указанной точке имеет максимум.

График указанной функции приведен выше. Построенная кривая называется Декартовым листом.

РАЗДЕЛ. Комплексные числа.