Постановка задачи: Пусть 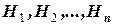 - полная система (группа) попарно несовместных событий (гипотез) т. е.
- полная система (группа) попарно несовместных событий (гипотез) т. е.

и пусть событие  может произойти лишь совместно с каким - либо одним из этих событий (гипотез) - ситуация аналогичная той, которая была ранее. И пусть
может произойти лишь совместно с каким - либо одним из этих событий (гипотез) - ситуация аналогичная той, которая была ранее. И пусть 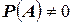 . Требуется найти условную вероятность
. Требуется найти условную вероятность 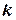 - ой гипотезы при условии, что событие
- ой гипотезы при условии, что событие  произошло, т.е.
произошло, т.е. 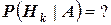 - переоценка гипотез.
- переоценка гипотез.
По теореме об умножении вероятностей
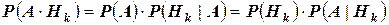 .
.
Следовательно
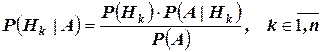 .
.
Или, с учетом того, что 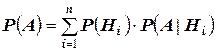 , можем записать:
, можем записать:
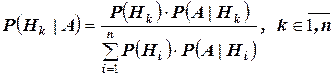 .
.
Полученная формула называется формулой Байеса (Бейеса) для переоценки гипотез. Другими словами: вероятность 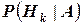 гипотезы после испытания равна произведению вероятности
гипотезы после испытания равна произведению вероятности 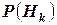 гипотезы до испытания на соответствующую ей условную вероятность
гипотезы до испытания на соответствующую ей условную вероятность 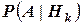 события, происшедшего при испытании, деленному на полную вероятность
события, происшедшего при испытании, деленному на полную вероятность 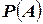 этого события.
этого события.

|
ПРИМЕР. При обследовании больного имеется подозрение (т.е. делаются предположения или, что то же самое, выдвигаются гипотезы) на одно из двух заболеваний 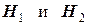 . Их вероятности в данных условиях равны
. Их вероятности в данных условиях равны 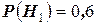 и
и 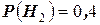 соответственно. Для уточнения диагноза назначается обследование, результатом которого будет отрицательная или положительная реакция. В случае болезни
соответственно. Для уточнения диагноза назначается обследование, результатом которого будет отрицательная или положительная реакция. В случае болезни 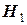 вероятность положительной реакции равна 0,9, а в случае болезни
вероятность положительной реакции равна 0,9, а в случае болезни 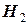 эта вероятность равна 0,5.
эта вероятность равна 0,5.
Обследования проведены дважды и оба раза реакция оказалась отрицательной. Найти вероятность каждого заболевания.
Решение. Во - первых, очевидно, что события 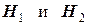 образуют полную группу событий. Действительно, эти события несовместны, так как у больного имеется подозрение только лишь на одно из двух заболеваний и сумма
образуют полную группу событий. Действительно, эти события несовместны, так как у больного имеется подозрение только лишь на одно из двух заболеваний и сумма 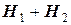 событий - есть достоверное событие (обследуемый болен):
событий - есть достоверное событие (обследуемый болен): 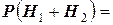
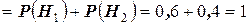 . Во - вторых, если обозначить через
. Во - вторых, если обозначить через  событие, которое состоит в том, что оба обследования дали отрицательный результат, то
событие, которое состоит в том, что оба обследования дали отрицательный результат, то 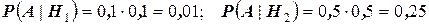 . Таким образом, нетрудно видеть, что
. Таким образом, нетрудно видеть, что
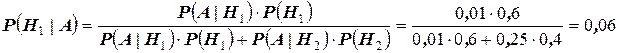 ;
;
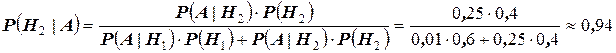 .
.
Как видим, при данных результатах обследования следует предполагать болезнь 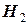 .
.
 2014-02-24
2014-02-24 4079
4079
