Линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
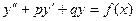 (9)
(9)
где p и q – данные постоянные числа или непрерывные функции от x, f(x) – правая часть уравнения, известная функция от x.
Теорема. Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения данного неоднородного уравнения, т.е. 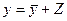 (10)
(10)
Общее решение 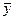 однородного линейного дифференциального уравнения с постоянными коэффициентами можно найти, остается лишь указать способ нахождения частного решения Z соответствующего неоднородного уравнения.
однородного линейного дифференциального уравнения с постоянными коэффициентами можно найти, остается лишь указать способ нахождения частного решения Z соответствующего неоднородного уравнения.
Рассмотрим несколько случаев отыскания частных решений уравнения (10) методом неопределенных коэффициентов.
3.1. Правая часть уравнения (10) – показательная функция: 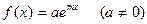 (11)
(11)
Ищем частное решение Z также в форме показательной функции 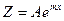 , где А – неопределенный коэффициент.
, где А – неопределенный коэффициент. 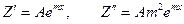 .
.
Подставляя 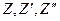 в (9) получим
в (9) получим
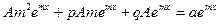 ;
; 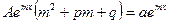 .
.
Сокращаем на 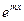 , то
, то 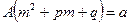
Возможны два случая:
а) m – не является корнем характеристического уравнения, т.е. 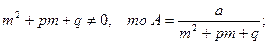 (12)
(12)
тогда 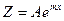 , вместо А подставляя (12), получим
, вместо А подставляя (12), получим
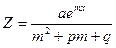 (13)
(13)
б) m – простой корень характеристического уравнения 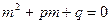 , тогда (10) не имеет частного решения в форме
, тогда (10) не имеет частного решения в форме 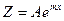 . В этом случае решение следует брать в более сложной форме
. В этом случае решение следует брать в более сложной форме 
 (14)
(14)
Пример 1. 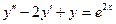 ;
; 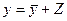
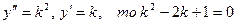 - характеристическое уравнение соответствующего однородного уравнения
- характеристическое уравнение соответствующего однородного уравнения
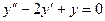 .
.
Решим характеристическое уравнение: 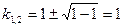
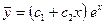 - общее решение соответствующего однородного уравнения.
- общее решение соответствующего однородного уравнения.
m=2 не является корнем характеристического уравнения, значит 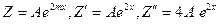
Подставляем в данное уравнение:
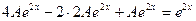 ;
; 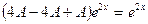 ;
; 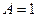 Значит, частное решение
Значит, частное решение 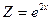 .
.
Общее решение данного уравнения 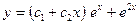
3.2. Правая часть неоднородного уравнения (10) – тригонометрический полином
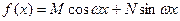 (15)
(15)
Ищем частное решение Z этого уравнения также в форме тригонометрического полинома.
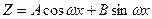
где A и B – неопределенные коэффициенты.
Дифференцируя, получим
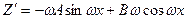
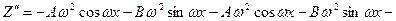
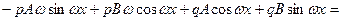
=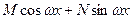
Собирая вместе члены с 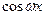 и
и 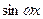 , имеем:
, имеем:
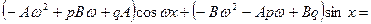
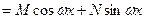
Так как последнее выражение представляет собой тождество, то его коэффициенты при 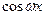 и
и 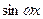 в левой и правой частях должны быть соответственно равны друг другу.
в левой и правой частях должны быть соответственно равны друг другу.
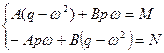
Из этой системы определяем коэффициенты A и B.
Возможны три случая:
1) 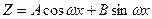
если ω±bi не является корнем характеристического уравнения.
2) 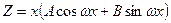
если ω±bi является простым корнем.
3) 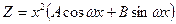
если ω±bi – кратный корень характеристического уравнения.
Пример. 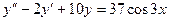
Решение. Составляем характеристическое уравнение


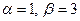 . Находим общее решение
. Находим общее решение 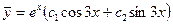 .
.
Частное решение Z данного неоднородного уравнения, соответственно его правой части 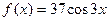 , ищем в виде:
, ищем в виде: 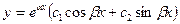
В формуле 
 ,
, 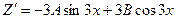 ,
,
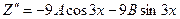 . Подставляя
. Подставляя  в данное неоднородное уравнение, получим
в данное неоднородное уравнение, получим
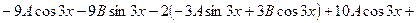
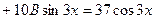
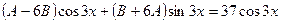
отсюда 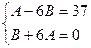
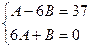
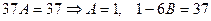 ,
, 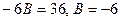 .
.
Следовательно, 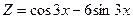
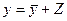 ;
; 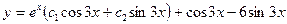
3.3. Правая часть линейного уравнения (10) представляет собой полином, например, второй степени
 (16)
(16)
Ищем частное решение Z также в форме полинома второй степени 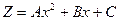
A, B, C – неопределенные коэффициенты.
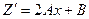 ,
, 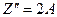
Подставляя 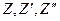 в (9), получим
в (9), получим
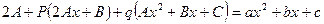
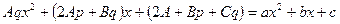
Коэффициенты при одинаковых степенях переменных x равны, то имеем систему:

Если 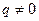 , то из этой системы для A, B, C получаются определенные числовые значения. Тем самым Z будет вполне определено.
, то из этой системы для A, B, C получаются определенные числовые значения. Тем самым Z будет вполне определено.
Если 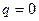 , то система несовместна. В этом случае, полагая, что
, то система несовместна. В этом случае, полагая, что 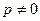 , частное решение Z следует искать в форме
, частное решение Z следует искать в форме 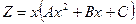
Аналогично нужно поступать, если 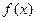 - полином какой-нибудь другой степени.
- полином какой-нибудь другой степени.
Произвольные постоянные, входящие в общее решение, могут быть определены из начальных условий.
Пример. Найти решение y уравнения 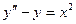 ,
,
такое, что 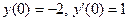
Решение.
Однородное уравнение 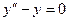
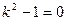 - характеристическое уравнение
- характеристическое уравнение
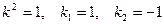
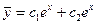 - общее решение соответствующего однородного уравнения
- общее решение соответствующего однородного уравнения
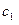 и
и 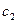 - постоянные.
- постоянные.

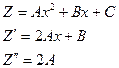
 Подставляя
Подставляя 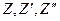 в данное уравнение, получим
в данное уравнение, получим

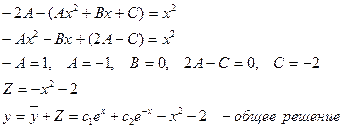
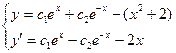
Используем начальные условия.
Полагая, 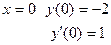
Для определения с1 и с2 получим систему
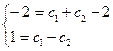
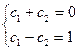
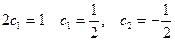 .
.
Эти значения с1 и с2 подставляем в общее решение данного дифференциального уравнения, имеем
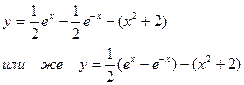
Тестовые вопросы для самоконтроля знаний.
1. Общий вид дифференциального уравнения n-го порядка:
A)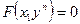 ; B)
; B)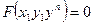 ; C)
; C)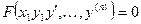 ;
;
D)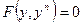 ; E)
; E)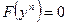
2. Общее решение дифференциального уравнения n-го порядка имеет вид:
A) 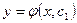 ; B)
; B) 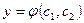 ; C)
; C) 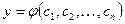 ;
;
D) 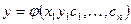 ; E)
; E) 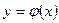
3. Общее решение дифференциального уравнения первого порядка 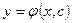 геометрически будет:
геометрически будет:
А) прямая линия; В) парабола; С) гипербола;
D) однопараметрическое семейство интегральных кривых
Е) кубическая парабола.
4. Линейные дифференциальные уравнения первого порядка имеют вид:
A) 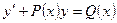 ; B)
; B) 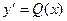 ; C)
; C) 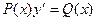 ;
;
D) 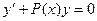 ; E)
; E) 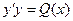 .
.
5. Если характеристическое уравнение имеет два различных действительных корня 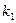 и
и 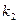 , то общее решение уравнения
, то общее решение уравнения 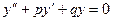 имеет вид:
имеет вид:
A) 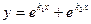 ; B)
; B) 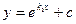 ; C)
; C) 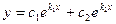 ;
;
D) 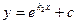 ; E)
; E) 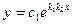
Решите следующие дифференциальные уравнения
6. 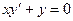
A)  ; B)
; B) 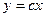 ; C)
; C) 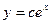 ; D)
; D) 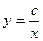 ; E)
; E) 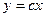
7. 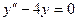
A) 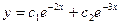 ; B)
; B) 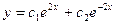 ;
;
C) 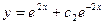 ; D)
; D) 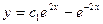 ;
;
E) 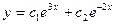
8. 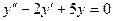
A)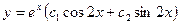 ; В)
; В) 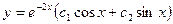
C)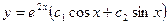 ; D)
; D)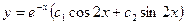
E) 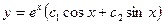
9. 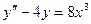
A) 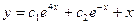 ; B)
; B) 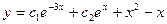 ;
;
C) 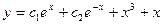 ; D)
; D) 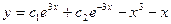 ;
;
E) 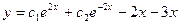
10. 
A) 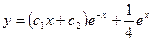 ; B)
; B) 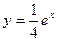 ;
;
C) 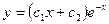 ; D)
; D) 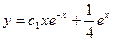 ;
;
E) 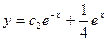
 2014-02-24
2014-02-24 1007
1007
