Кинематика материальной точки и твердого тела

Требования к оформлению РГР

Каждую расчетно-графическую работу следует выполнять в отдельной тетради, на обложке которой указывают номер работы, вариант, кем работа выполнена, кто ее проверил, дату сдачи на проверку; например, согласно следующему образцу:

Физика 1 РГР №__ Вариант №__

Выполнил студент ___(Ф.И.О, группа)

Проверил ___(Ф.И.О. преподавателя)

Сдана на проверку ___(дата)

Работу выполняют шариковой (или иной) ручкой, рисунки - при по­мощи карандаша и линейки.

Условие задачи следует переписывать полностью, без сокращений. За­тем его записывают с помощью общепринятых символических обозначений в краткой форме, под заглавием «Дано». Если в задаче заданы числовые вели­чины, то необходимо выразить их в системе единиц СИ.

Решение каждой задачи необходимо сопроводить пояснениями, рас­крывающими смысл и значение используемых обозначений, указать физиче­ские законы и принципы, положенные в основу решения. Необходимо обос­новывать применение в каждом конкретном случае того или иного закона, принципа или соотношения. После того, как задача решена в общем виде, т.е. получен ответ в виде расчетной формулы, производят вычисления, руково­дствуясь при этом правилами приближенных вычислений.

Основные понятия, законы, соотношения

Радиус-вектор r точки, его компоненты. Закон движения частицы. Траектория движения. Векторы скорости v и ускорения а, их компоненты. Тангенциальное 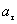, нормальное 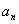и полное а ускорения. Радиус кривиз­ны траектории .

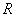Угол поворота 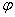при вращении твердого тела. Угловая скорость ω. Угловое ускорение ε. Связь между угловой ω и линейной скоростями v, между угловым 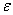и тангенциальным 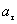ускорениями.

[1] §§2-5; [2] §§1-4.

Прямая основная задача кинематики заключается в нахождении любо­го параметра движения ( v, а, ω, ε ) по известному закону движения r = r (t) или .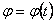

Метод решения основной задачи кинематики состоит в последователь­ном применении определений кинематических величин и соотношений, свя­зывающих эти величины. Зная закон движения, можно определить любой параметр движения.

Пример 1.

Радиус-вектор частицы изменяется со временем по закону r (t) = 3t² i +2t j +4 k (м). Найти скорость v, ускорение а и модуль скорости v для произвольного момента времени .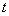

Решение. Запишем компоненты радиус-вектора и получим кинематические уравнения движения:

x(t) =3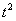 (м), y(t) =2 t (м), z(t) =4 (м)

Согласно определению, скорость – это первая производная по времени от радиус-вектора, а ее компоненты – первые производные от соответствующих координат:

v_x = 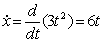(м/с); v_y =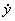==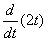2(м/с); v_z =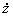=0.

Ускорение, согласно определению, - это первая производная по времени от скорости:

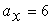(м/с²) , .

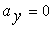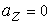Таким образом: v =6 t i +2 j, a =6 i.

Модуль любого вектора, как известно, равен корню квадратному из суммы его компонентов. Соответственно, модули векторов скорости и ускорения будут равны:

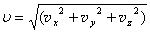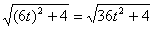= (все – в м/с), a =6 (м/с²).

Пример 2.

Обратная задача кинематики заключается в определении закона движения по какому-либо известному параметру движения и заданным на­чальным условиям.

Метод решения обратной задачи также основан на применении зако­нов кинематики, но вместо дифференцирования по времени t, теперь выпол­няется интегрирование дифференциальных уравнений. Появляющиеся при этом константы интегрирования находят из начальных условий.

Пример 3.

Поезд движется прямолинейно со скоростью 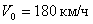. Внезапно на пути возникает препятствие, и машинист включает тормозной механизм. С этого момента скорость поезда изменяется по закону 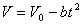, где 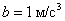. Каков тормозной путь поезда? Через какое время после начала торможения он остановится?

Решение:

Т.к. движение одномерное, то для нахождения закона его движения достаточно найти закон изменения одной координаты, например, 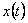.Согласно определению скорости: ,

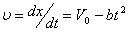или .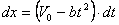

Интегрируя последнее уравнение, получим:

.

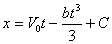Чтобы определить константу интегрирования 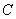, воспользуемся начальными условиями: при 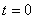, , 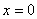которые подставим в закон движения. В результате получим 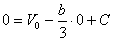, откуда следует, что .

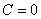Время 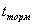торможения поезда до его остановки найдем из уравнения

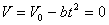, откуда .

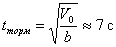Тормозной путь равен: .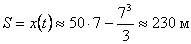

2Основная задача динамики и методы ее решения для частицы, системы частиц и твердого тела

Основные понятия, законы, соотношения

Масса. Импульс. Сила. Первый закон Ньютона. Инерциальные системы отсчета. Второй закон Ньютона (две формулировки). Третий закон Ньютона.

Центр масс системы частиц. Движение центра масс твердого тела.

Момент силы, плечо силы. Момент импульса. Уравнение моментов. Момент инерции тела относительно оси. Уравнение динамики вращательно­го движения твердого тела относительно неподвижной оси.

[1] §§ 6, 8, 10, 30, 31; [2] §§ 5-7, 9, 16, 18, 19.

Основная задача динамики заключается в определении механического состояния системы в произвольный момент времени по заданным силам и состоянию системы в начальный момент времени.

Метод решения основной задачи динамики базируется на применении соответствующих рассматриваемой системе законов динамики. Интегриро­ванием полученных при этом уравнений движения находят зависимости Р (t) и L (t), которые показывают, как в процессе движения изменяются, соответственно, импульс и момент импульса частицы или твердого тела.

Пример 4.

Частице массой 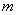сообщена начальная скорость 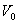под уг­лом а к горизонту. Траектория полета частицы лежит в плоскости 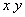. Пре­небрегая сопротивлением воздуха, найти зависимость от времени:

а) импуль­са частицы ;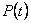

б) момента импульса 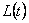частицы относительно точки бросания 0.

Решение:

Движение материальной точки подчиняется законам динамики

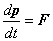, (2.1)

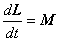. (2.2)

Тело, брошенное под углом к горизонту, описывает параболическую траекторию (рисунок 1).

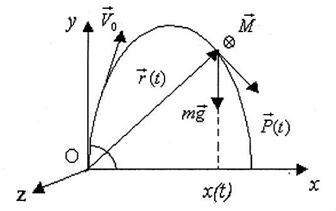
Рисунок 1

Единственная сила, действующая на тело, - это сила тяжести, поэтому,

d p =m g ·dt (2.3)

интегрируя дифференциальное уравнение (2.3), получим:

p (t)- p ₀ = - m g t, или:

p (t) = m V ₀ - m g t (2.4)

Момент силы, по определению, равен векторному произведению радиус-вектора точки приложения силы на вектор силы:

=.

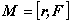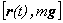Векторное произведение двух векторов всегда перпендикулярно плоскости, в которой лежат сомножители, в данном случае - момент силы тяжести перпендикулярен плоскости 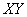, вдоль отрицательного направления оси 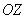. Модуль момента силы равен произведению силы на плечо (кратчайшее расстояние от точки 0 до линии действия силы, которое в нашем случае равно координате 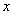тела): M= mgx(t).

Таким образом,

M (t)= - j mgx(t). (2.5)

Подставив полученное выражение в (2.2):

d L = - j mgx(t)·dt. (2.6)

Интегрированием получим искомый результат:

L (t)= - j mgV₀ t²cosα (2.7)

Второй общий метод решения задач динамики состоит в опреде­лении ускорения частицы или центра масс твердого тела. В этом случае необходимо выполнить следующие действия:

▪ выяснить, с какими телами взаимодействует рассматриваемое тело, найти величину, направление и точку приложения каждой из сил;

▪ сделать схематический рисунок и указать на нем направление каждой из приложенных сил и ускорения;

▪ выбрать инерциальную систему отсчета и записать для рассматриваемого тела уравнение динамики в векторной форме:

m a = F _{+ F ₂+...+ F _N. (2.8)

Если силы действуют не по одной прямой, то выбирают две взаимно перпендикулярные ос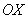и и 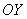. Спроектировав все векторы, входящие в векторное уравнение на эти оси, записывают второй закон Ньютона в виде двух скалярных уравнений:

ma_x = ΣF_ix,

ma_y = ΣF_iy, (2.9)

Если задано криволинейное движение, то одну из осей направляют вдоль касательной к траектории, а другую – по нормали к ней.

Если в задаче рассматривается движение системы связанных между
собой тел, то следует уравнение движения записать для каждого тела в от­дельности. Затем записывают в виде уравнений кинематические условия,
связывающие ускорения отдельных тел системы.

Проверив, совпадает ли число неизвестных с числом уравнений, решают полученную систему уравнений.

После того, как найдено ускорение частицы (или центра масс твердого
тела), определение скорости (импульса) и закона движения сводится к решению обратной задачи кинематики.