Передаточные функции импульсных автоматических систем

Изображение часто встречающихся функций времени

Контрольные вопросы

1. Чем отличается дискретное преобразование Лапласа от обычного преобразования Лапласа?

2. Как получаются Z-изображения функций времени?

3. Что дает разработчику или исследователю автоматических систем использование обычного и дискретного преобразований Лапласа и Z-преобразования?

Структурные представления и передаточные функции составляют основу для инженерных расчетов импульсных автоматических систем. Они позволяют в значительной степени облегчить решение задач исследования.

Для исследования динамических свойств системы в первую очередь необходимо определить ее передаточные функции, которые, как известно, устанавливают зависимость между входным воздействием и реакцией системы (звена). Обычно в рассмотрение вводят, как и при исследовании непрерывных систем, следующие передаточные функции: передаточную функцию разомкнутой импульсной системы и передаточную функцию ошибки.

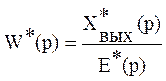Передаточной функцией разомкнутой импульсной системы называется отношение изображений в смысле дискретного преобразования Лапласа выходного и входного импульсных сигналов при нулевых начальных условиях:

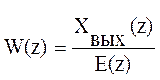.Аналогично определяется эта передаточная функция в смысле Z - преобразования:

Основная задача состоит в том, чтобы определить передаточную функцию W(z) по известной передаточной функции приведенной непрерывной части системы W(p). Эту задачу решают в следующей последовательности:

1. По передаточной функции W(p) в результате применения обратного
преобразования Лапласа находят функцию веса ПНЧ:

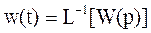2. По функции веса ПНЧ w(t) определяют аналитическое выражение
для соответствующей дискретной функции веса w(пТ).

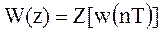3. Искомую передаточную функцию W(z) получают как Z - преобразование дискретной функции веса ПНЧ:

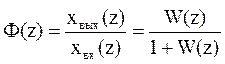Основная передаточная функция замкнутой импульсной системы позволяет вычислить реакцию замкнутой системы х_вых(пТ) на задающее воздействие х_вх(пТ). Ее определяют, как и в непрерывных системах, в соответствии с уравнением замыкания через дискретную передаточную функцию разомкнутой системы:

	(3.14)

Передаточную функцию замкнутой системы всегда можно представить в виде отношения двух полиномов относительно переменной z.

		(3.15)

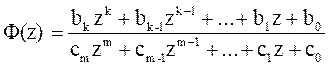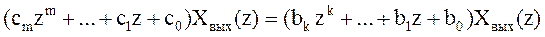Запишем это выражение в развернутом виде:

(3.16)

Левая часть этого уравнения (в скобках) представляет собой характеристический полином замкнутой импульсной системы М (z).

В результате перехода от изображений к оригиналам в формуле (16) легко получить соответствующее разностное уравнение системы:

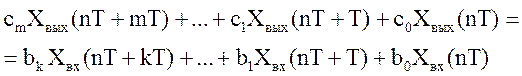Аналогично можно получить разностное уравнение разомкнутой системы по передаточной функции W(z).

Передаточная функция ошибки определяется через передаточную функцию разомкнутой системы по формуле

		(3.17)

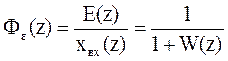Зная задающее воздействие и эту передаточную функцию, можно оценить динамическую точность импульсной системы — найти дискретную функцию ошибки ε(nT).

Рассмотрим конкретный пример определения передаточных функций импульсной системы. Определим передаточные функции системы, структурная схема которой изображена на рис. 3.12.

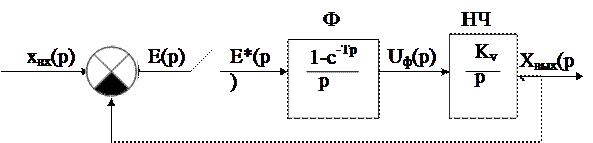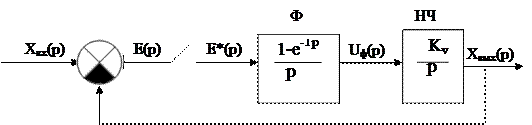Рис. 3.12. Структурная схема импульсной системы

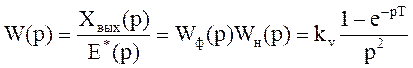Как видно из рисунка, в прямой цепи системы имеется простейший импульсный элемент (фиксатор) и непрерывная часть (интегрирующее звено). Передаточная функция приведенной непрерывной части:

Дискретную передаточную функцию разомкнутой системы находим в соответствии с методикой, изложенной выше:

		(3.18)

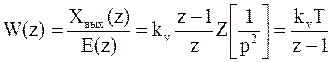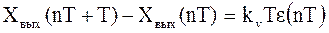Разностное уравнение разомкнутой системы определяем, в случае необходимости, непосредственно из формулы (3.18):

Зная W (z), легко найти основную передаточную функцию замкнутой системы:

		(3.19)

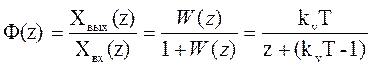и передаточную функцию ошибки:

		(3.20)

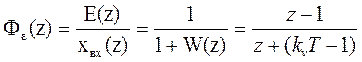Динамические процессы в замкнутой импульсной системе описываются следующим разностным уравнением, полученным из формулы (3.19) путем перехода к оригиналам:

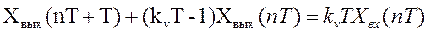Контрольные вопросы

1. Какие передаточные функции обычно используют при исследовании
импульсных систем радиоавтоматики и почему?

2. Как определяют передаточную функцию замкнутой импульсной сис
темы?

3. Как определяется дискретная передаточная функция ошибки и для чего она используется?