Воздействиях. Моделирование систем

СТАЦИОНАРНЫХ СИСТЕМ ПРИ ДЕТЕРМИНИРОВАННЫХ

АНАЛИЗ КАЧЕСТВА ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ

Лекция 6

6.1 Показатели качества процесса управления и требования к ним

требование устойчивости линейной стационарной системы означает, что переходная составляющая процесса управления должна затухать. Однако это требование является далеко не достаточным условием ее практической пригодности. Требуется еще, во-первых, чтобы управляемая величина в установившемся режиме была достаточно близка к заданному значению, во-вторых, чтобы затухание переходного процесса было достаточно быстрым, а отклонения (колебания) управляемой величины в переходном процессе были невелики. поэтому при проектировании системы решается не только задача обеспечения ее устойчивости, но и задача обеспечения требуемого (заданного) качества процесса управления, в понятие которого входят точность работы системы в установившихся режимах и качество переходного процесса.

Величины, характеризующие поведение системы в установившемся и переходном процессах при определенном виде внешнего воздействия, принято называть показателями качества процесса управления (показателями качества системы).

В подавляющем большинстве практических задач исследование качества системы производится при детерминированных воздействиях.

Основным показателем качества работы системы в установившемся режиме является точность, оцениваемая величиной установившейся ошибки при различных типовых внешних воздействиях. Эту ошибку, в отличие от инструментальной (приборной), называют методической (структурной) ошибкой. Ее можно определить с помощью теоремы о конечном значении и коэффициентов ошибок.

К основным показателям качества переходного процесса относятся время регулирования, перерегулирование, число и частота колебаний управляемой (регулируемой) величины. Эти показателя часто определяются из графика переходной функции по задающему воздействию (см. рис. 6.1).

Рисунок 6.1

Время регулирования t_р. Под временем регулирования понимается время t_р, за которое переходный процесс практически заканчивается. Момент окончания переходного процесса определяется по уменьшению абсолютного значения разности | h(t) – h_y | до допустимо малой величины ∆. Величину ∆ обычно принимают равной 0,05 h_y. Время регулирования определяет длительность переходного процесса, т.е. ее быстродействие. Чем меньше t_р, тем быстрее наступает установившийся режим.

Перерегулирование σ. Перерегулированием σ называется максимальное отклонение управляемой величины от установившегося значения, выраженное в процентах:

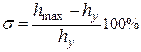
Перерегулирование в системах не должно быть слишком большим. При большой величине σ возможны значительные динамические ошибки и динамические усилия в механических частях систем или чрезмерные перенапряжения в электрических элементах. Для многих САУ условия работы требуют, чтобы величина перерегулирования не превышала 10-30 %. В некоторых случаях требуется, чтобы переходный процесс протекал вообще без перерегулирования, т.е. был монотонным; в ряде случаев может допускаться перерегулирование 50-70 %.

Число колебаний N_h. Под числом колебаний N_h понимается количество колебаний управляемой величины за время переходного процесса около ее установившегося значения. Число колебаний характеризует колебательность системы. Если N_h > 1, то переходный процесс называют колебательным. Малоколебательные переходные процессы характеризуются наличием N_h ≤ 1. системы, обладающие колебательными и малоколебательными переходными процессами, называют системами с перерегулированием.

Обычно приемлемым числом колебаний в САУ считается 1-2. однако, бывают системы, в которых колебательность не допускается совсем. С другой стороны, в ряде систем иногда допускается три и более.

Частота колебаний f_h. Частоту колебаний можно определить по формуле:

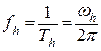
где T_h – расстояние между двумя смежными максимумами, условно называемое периодом колебаний.

Число колебаний связано с периодом колебаний и временем регулирования следующим примерным соотношением:

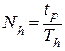
Требования к показателям качества переходного процесса можно представить графически в виде некоторой допустимой области протекания переходного процесса, за пределы которой управляемая величина не должна выходить (см. рис. 6.2).

Рисунок 6.2

Следует иметь в виду, что к качеству переходного процесса могут предъявляться и другие требования, например, время нарастания первого максимума t_m, максимальное ускорение управляемой величины на начальном участке нарастания h(t), т.е. h_мах(t) при 0< t< t_m и т.д.

6.2 анализ точности систем в установившемся режиме

при типовых воздействиях

6.2.1 вывод общих расчетных формул

для определения установившихся ошибок

рассмотрим этот вопрос применительно к САУ, на входах которой действует задающее Х(t) и возмущающее f(t) воздействия (рис. 6.3), а качестве выходной величины выступает ошибка ε(t).

Согласно теореме о конечном значении, можно записать

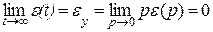(6.1)

F(р)

где ε_у – установившаяся ошибка системы; ε(р) – изображение по Лапласу ошибки ε(t).

	Х(р)		САУ		ε(р)

рисунок 6.3

ранее было показано (см. лекцию 4), что при одновременном действии на систему (рис. 6.3) задающего Х(р) и возмущающего f(р) воздействий изображение ошибки ε(р) определяется выражением

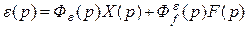
Подставляя его в (6.1) получим общую расчетную формулу

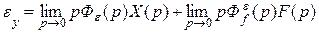(6.2)

Из этой формулы следует, что ошибка САУ в установившемся режиме зависит от структуры системы и характера внешних воздействий и имеет две составляющие:

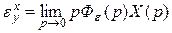; (6.3)

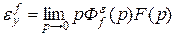(6.4)

Составляющая 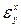является ошибкой воспроизведения задающего воздействия Х(t) при f(t) = 0. эту ошибку принято называть ошибкой по задающему воздействию. Составляющая обусловлена действием возмущения f(t) при Х(t) = 0 и называется ошибкой по возмущающему воздействию.

6.2.2 вывод расчетных формул для установившихся

ошибок САУ с единичной ООС

F(p)

структурно-динамическая схема САУ с единичной ООС показана на рис. 6.4.

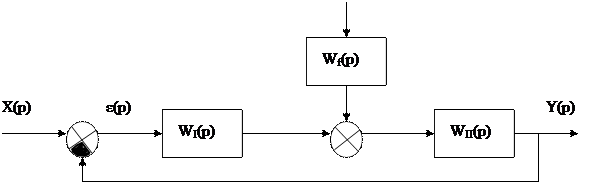
Рисунок 6.4

В общем случае передаточные функции W_I(р), W_II(р), W(р) = W_I(р)W_II(р) и W_f(р) можно представить в виде:

;

,

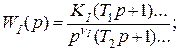
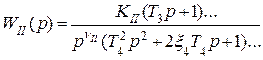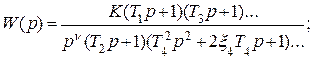
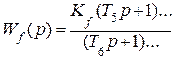где К_I – коэффициент передачи управляющего устройства, а в более общем случае – коэффициент передачи участка цепи между входом системы и точкой приложения возмущения; К_II – коэффициент передачи объекта управления, а в более общем случае – коэффициент передачи участка цепи между точкой приложения возмущения и выходом системы; К_f – коэффициент передачи звена, через которое возмущение поступает на сумматор; К = К_IК_II – коэффициент передачи разомкнутой системы; ν_I, ν_II, ν = ν_I + ν_II – количество интегрирующих звеньев в W_I(р), W_II(р), W(р). В передаточной функции W_f(р), как правило, интегрирующих звеньев нет.

В соответствии с СДС (рис. 6.4) определим передаточные функции Ф_ε(р), 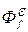(р):

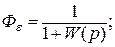
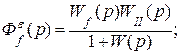(6.5)

Подставим (6.5) в формулы (6.3) и (6.4), получим

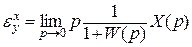(6.6)

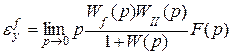(6.7)

Учитывая, что

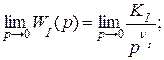
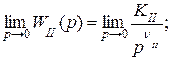
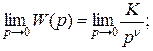
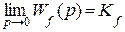
выражения (6.6), (6.7) примут вид:

;

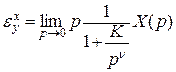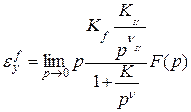
или окончательно

;

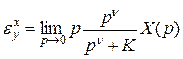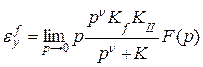
из формул (6.8) и (6.9) видно, что установившиеся ошибк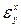и и замкнутой САУ зависят как от характера внешних воздействий и величины коэффициентов К_I, К_II, К_f, так и от количества и места расположения интегрирующих звеньев в одноконтурной структурно-динамической схеме исследуемой системы.

Определим значения установившихся ошибок 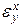, 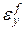замкнутой САУ с различной наиболее характерной структурой.

6.2.3 Определение установившихся ошибок

статистических систем

статистическая система характеризуется отсутствием интегрирующих звеньев в разомкнутой цепи, т.е. в статической системе ν_I = ν_II – ν = 0. в этом случае выражения (6.8) и (6.9) принимают вид:

; (6.10)

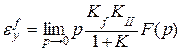(6.11)

Определим установившиеся ошибки при различном характере входных воздействий:

а) постоянные (ступенчатые) входные воздействия, т.е.

Х(t) = Х₀1(t); f(t) = f₀1(t) или Х(р) = 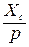; f(р) =

Подставляя Х(р) и f(р) в (6.10) и (6.11), получим:

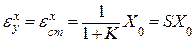; (6.12)

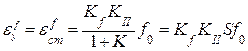(6.13)

где S = 1/(1 + К) – коэффициент статизма системы.

Формулы (6.12) и (6.13) подтверждают тот факт, что при отсутствии в одноконтурной структурно-динамической схеме интегрирующих звеньев САУ будет статической. Из этих формул видно, что статические ошибки по задающему и возмущающему воздействиям пропорциональны величине этих воздействий и коэффициенту статизма системы, который тем меньше, чем больше коэффициент усиления К разомкнутой системы. Формула (6.13) дает основание утверждать, что статические ошибк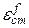и , и 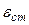=+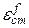можно уменьшить только за счет увеличения коэффициента передачи участка цепи от входа системы до точки приложения внешнего воздействия. Увеличение К₁ приводит увеличению коэффициента К разомкнутой системы и уменьшение коэффициента статизма S = 1/(1 + К). однако при этом следует помнить, что с увеличением коэффициента уменьшается запас устойчивости системы и при К > К_кр система оказывается неустойчивой;

б) скоростные входные воздействия, т.е. Х(t) = V_xt, f(t) = V_ft, или Х(р) = V_x/р², f(р) = V_f/р².

Подставляя Х(р) и f(р) в (6.10) и (6.11), получим 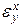= ∞, = ∞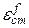. Это значит, что установившиеся ошибк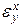и и 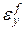статистических систем, создаваемые внешними воздействиями, изменяющимися с постоянной скоростью, со временем t → ∞ увеличивается до бесконечности. Следовательно, САУ можно проектировать статическими в том случае, если они работают в условиях постоянных внешних воздействий или внешних воздействий, близких к постоянным.

6.2.4 Определение установившихся ошибок астатических систем

А. астатическая САУ с ν_I = 0, ν_II = 0 и ν = ν_I + ν_II = 1, т.е. САУ, содержащая одно интегрирующее звено до точки приложения возмущения:

а) постоянные входные воздействия, т.е. Х(t) = Х₀1(t), f(t) = f₀1(t) или Х(р) = Х₀/р f(р) = f₀/р. Подставляя ν = I, ν_I = 1, Х(р) и f(р) в (6.8) и (6.9), получим = 0, 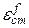= 0. следовательно, САУ с такой структурой является астатической первого порядка по отношению к задающему и возмущающему воздействиям;

б) скоростные входные воздействия, т.е. Х(t) = V_х t, f(t) = V_f t или Х(р) = V_х/р², f(р)= V_f/р². подставляя ν = 1, ν_I = 1, Х(р) и f(р) в (6.8) и (6.9), получим:

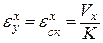; (6.14)

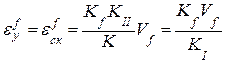(6.15)

где К = К_IК_II коэффициент передачи разомкнутой системы, имеющий размерность с^-1, называемой добротностью системы по скорости.

Установившуюся ошибку воспроизведения скоростного воздействия принято называть скоростной ошибкой, поэтому в формулах (6.14) и (6.15) принято обозначение 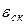. Из формул (6.14) и (6.15) видно, что установившиеся ошибки , 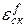и, следовательно, 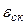= 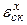+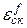, создаваемые внешними воздействиями, изменяющимися с постоянной скоростью, можно уменьшить за счет увеличения коэффициента К₁. Увеличение этого коэффициента приводит, во-первых, к уменьшению 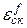и, во-вторых, к увеличению коэффициента К, а значит к уменьшению 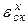. Однако, как уже отмечалось, такой способ повышения точности САУ связан с ухудшением ее устойчивости;

в) равноускоренные входные воздействия, т.е. Х(t) = а_х t², f(t) = а_f t² или Х(р) = 2а_х/р³, f(р)= 2а_f/р³. подставляя ν = 1, ν_I = 1, Х(р) и f(р) в (6.8) и (6.9), получим: = ∞, = ∞.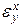

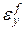Это значит, что внешние воздействия, изменяющиеся с постоянным ускорением, создают установившиеся ошибк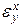и и 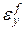, которые со временем t → ∞ увеличиваются до бесконечности.

Следовательно, САУ, содержащие в одноконтурной структурно-динамической схеме одно интегрирующее звено до точки приложения возмущения, будут выполнять свои функции в том случае, если внешние воздействия постоянны или изменяются с постоянной скоростью. Примерами таких САУ могут служить следящие системы, работающие в режиме слежения с постоянной скоростью, системы программного обеспечения, к которых Х_пр(t) изменяется по закону, близкому к скоростному воздействию, а также системы стабилизации, к которым предъявляются требования, чтобы 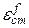= 0.

Б. астатическая САУ ν_I = 0, ν_II = 1 и ν =ν_I + ν_II = 1, т.е. САУ, содержащая одно интегрирующее звено за точкой приложения возмущения:

а) постоянные входные воздействия, т.е. Х(t) = Х₀1(t), f(t) = f₀1(t) или Х(р) = Х₀/р f(р) = f₀/р. Подставляя ν = 1, ν_I = 0, Х(р) и f(р) в (6.8) и (6.9), получим = 0, а

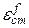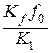= (6.16)

следовательно, САУ с такой структурой является астатической первого порядка по отношению к задающему воздействию, а по отношению к возмущению будет статической. При этом величина 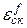этой САУ не равна 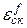статической САУ, что видно из сопоставления формул (6.13) и (6.16);

б) если к этой системе приложены одновременно задающее воздействие Х(t) = V_х t и возмущение f(t) = V_f t, то нетрудно убедиться в том, что 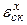= V_х/К, 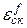= ∞ и, следовательно, 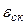= ∞. Это значит, что САУ с одним интегрирующим звеном, расположенным за точкой приложения возмущения, обеспечивает воспроизведение скоростного задающего воздействия с точностью, определяемой такой же скоростной ошибкой, что и система с одним интегрирующим звеном, расположенным до точки приложения возмущения. Однако, она неспособна скомпенсировать действие возмущения, изменяющегося с постоянной скоростью. Если к этой системе приложено задающее воздействие Х(t) = а_х t², т.е. задающее воздействие, изменяющееся с постоянным ускорением, то оно будет создавать 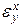= ∞. Поэтому, САУ с такой структурой могут найти применение для воспроизведения Х(t) = V_х t в условиях действия постоянных возмущений. Примером может служить следящая система, работающая в режиме слежения с постоянной скоростью при f(t) = const.

Анализ полученных выше результатов для двух астатических САУ с различным методом расположения одного интегрирующего звена позволяет сделать следующий очень важный для практики вывод: порядок астатизма системы по отношению к задающему воздействию определяется числом ν = ν_I + ν_II, т.е. числом интегрирующих звеньев, содержащихся в однокон-турной структурно-динамической схеме системы, а по отношению к возмущающему воздействию – числом ν_I, т.е. числом интегрирующих звеньев, расположенных между входом системы и точкой приложения этого возмущения.

В. В заключение рассмотрим определение ошибок 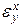, 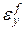САУ с ν_I = 1, ν_II = 1, ν = ν_I + ν_II = 2. эта система по отношению к задающему воздействию является астатической второго порядка (ν = ν_I + ν_II = 2), а по отношению к возмущению – астатического первого порядка (ν_I = 1). Поэтому при воздействиях Х(t) = V₀ 1(t), f(t) = f ₀ 1(t) имеем 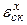= = 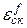0; при воздействиях Х(t) = V_х t, f(t) = V_f t точность работы этой системы будет определяться только 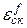= K_fV_f/K_I, т.к. наличие в одноконтурной структурно-динамической схеме двух последовательно соединенных интегрирующих звеньев приводит к тому, что 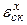= 0. если у этой системе будут приложены Х(t) = а_х t² и f(t) = а_f t², то, согласно формулам (6.8) и (6.9),

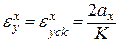(6.17)

а 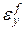= ∞. Это значит, что задающее воздействие, изменяющееся с постоянным ускорением а_х, создает постоянную установившуюся ошибку, величина которой определяется по формуле (6.17). эта ошибка характеризует точность воспроизведения системой равноускоренного воздействия. Ее принято называть ошибкой от ускорения, а коэффициент передачи К, входящий в формулу (6.17) и имеющий размерность с^-2 (ν = 2) – коэффициентом передачи (добротностью) системы по ускорению. Так как возмущающее воздействие, изменяющееся с постоянным ускорением а_f, создает установившуюся ошибку, стремящуюся к бесконечности, то САУ с такой структурой могут найти применение для воспроизведения Х(t) = а_хt² в условиях действия постоянных возмущений или возмущений, изменяющихся с постоянной скоростью. Примером может служить следящая система, работающая в режиме слежения с постоянным ускорением при постоянных возмущающих воздействиях и при возмущениях, изменяющихся с постоянной скоростью.

Нетрудно убедиться в том, что если на вход астатической системы с ν_I = 1, ν_II = 1 поступает задающее воздействие, описываемое кубической функцией времени, то 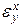= ∞. Это значит, что такое воздействие система воспроизвести не может. Для его воспроизведения с постоянной установившейся ошибкой необходимо ввести еще одно последовательное интегрирующее звено, т.е. создать астатическую систему третьего порядка.

На практике при оценке точности САУ с единичной ООС (определением установившихся ошибок) следует придерживаться следующего порядка решения задач:

а) определить порядок астатизма системы по отношению ко всем воздействиям (т.е. количество интегрированных звеньев ν_I, ν_II и ν);

б) определить, какой будет установившаяся ошибка при заданном воздействии (ноль, постоянная величина или бесконечность);

в) если ошибка равна постоянной величине, выбрать соответствующую формулу и определить численное значение ошибки.

6.3 Анализ качества переходного процесса

рассмотренные ранее показатели качества переходного процесса часто называются прямыми показателями, а методы, позволяющие построить переходную характеристику и определить по ней прямые показатели, - прямыми методами анализа. Основными из них являются: а) классический и операционный методы решения уравнений движения системы при Х(t) = 1(t) и нулевых начальных условиях; б) методы, основанные на использовании аналоговых и цифровых вычислительных машин (аналоговое и цифровое моделирование системы); в) приближенные методы построения переходной характеристики.

Из приближенных методов построения переходной характеристики наиболее широкое практическое применение получил разработанный в 1948 г. советским ученым В.В. Солодовниковым метод трапецеидальных частотных характеристик.

Кроме прямых методов анализа качества переходного процесса, в теории управления разработаны более удобные для инженерной практики косвенные методы оценки, часто называемые косвенными критериями качества переходных процессов. Они позволяют сравнительно просто, без построения кривой h(t), оценить не только качество системы, но и решать задачу выбора одного или нескольких параметров системы из условия обеспечения требуемого качества. В настоящее время существует следующие основные группы косвенных критериев качества: частотные, корневые и интегральные.

Наибольшее распространение получил косвенный метод оценки качества переходного процесса по вещественной ЧХ. Математической основой этого метода является связь между h(t) и ВЧХ Р(ω) системы.

6.4 Связь между ВЧХ и переходной функцией системы

при изучении частотных характеристик систем и их элементов (см. лекцию 2) отмечалось, что они представляют собой формулы и соответствующие им графики, характеризующие реакцию системы (элемента) на гармонический входной сигнал в установившемся режиме. Однако, несмотря на это, частотные характеристики определяют и динамические свойства систем (элементов). Объясняется это тем, что между частотными и временными характеристиками существует связь, устанавливаемая с помощью преобразования Фурье. Одностороннее преобразование Фурье характеризуется формулами:

;

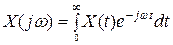и является частным случаем преобразования Лапласа при р = jω, т.е. оно применимо для функций Х(t), удовлетворяющих условиям: Х(t) = 0 при t < 0, < ∞.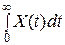

Ранее было показано, что w(t) = L [ Ф(р) ].

Поэтому, если САУ устойчива, то при р = jω получим

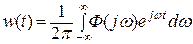, (6.18)

где Ф(jω)=w(jω)= 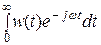представляет собой изображение Фурье и является комплексной функцией частоты ω, которая определяет гармонический состав функции w(t). Функция Ф(jω) может быть найдена из передаточной функции Ф(р) подстановкой р = jω. Выражение (6.18) с учетом того, что

;

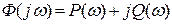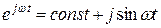
примет вид

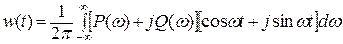
отбрасывая в этом выражении мнимую часть (так как w(t) является вещественной), будем иметь

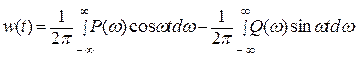(6.19)

Подынтегральные выражения Р(ω)cosωt и Q(ω)sinωt представляют собой четные функции частоты ω. Поэтому интегрирование в пределах (-∞, ∞) можно заменить на (0, ∞) и удвоить результат. В этом случае (6.19) примет вид

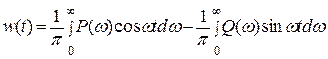(6.20)

Поскольку для момента времени t = -t, (т.е. t < 0) w (-t) = 0, cos(-ωt) = cosωt, sin(-ωt) = - sinωt, то можно, подставив в выражение (6.20) вместо t величину – t, записать

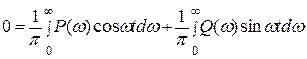(6.21)

Складывая выражения (6.20) и (6.21), получим

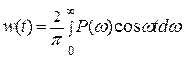(6.22)

Эта формула устанавливает связь между импульсной переходной функцией w(t) системы и ее ВЧХ р(ω). Учитывая, что

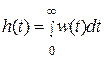
и интегрируя выражение (6.22), найдем

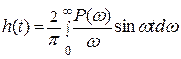(6.23)

т.е. найдем искомую связь между переходной функцией h(t) системы и ее ВЧХ Р(ω).

Если из выражения (6.20) вычесть выражение (6.21), то получим связь w(t) с Q(ω):

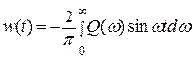(6.24)

Интегрируя (6.24) от 0 до t, найдем связь между h(t) и Q(t):

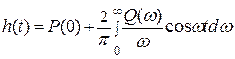(6.25)

где Р(0) – значение ВЧХ Р(ω) при ω = 0.

Полученные формулы (6.22) – (6.25) равноценны. Однако на практике особенно широко пользуются формулами, которые устанавливают связь w(t) и h(t) с Р(ω). В частности, формула (6.23) лежит в основе приближенного метода построения переходной характеристики h(t) САУ по известному графику ее ВЧХ Р(ω) и косвенного метода оценки качества переходного процесса САУ, вызванного задающим воздействием Х(t) = 1(t), по виду ВЧХ Р(ω).

Следует иметь ввиду, что временные характеристики w(t), h(t) имеют связь не только с ВЧХ Р(ω) и МЧХ Q(ω), но и с другими частотными характеристиками замкнутой и разомкнутой системы. Так, если в формулы (6.23) и (6.25) подставить Р(ω)=A(ω)cosφ(ω), Q(ω)=A(ω)sinφ(ω) и Р(0) = А(0), а затем формулы сложить, то после элементарных преобразований найдем:

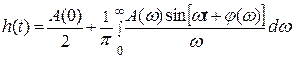(6.26)

если же в формулу (6.23) вместо Р(ω) подставить выражение

,

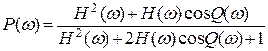то получим

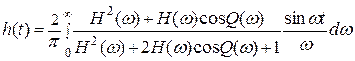(6.27)

формулы (6.26) и (6.27) устанавливают связь h(t) с амплитудно-частотными и фазо-частотными характеристиками замкнутой и разомкнутой системы, и, следовательно, указывает на возможность оценки качества переходного процесса, вызванного задающим воздействием Х(t) = 1(t), по виду АЧХ и ФЧХ системы, как в замкнутом, так и в разомкнутом состоянии.

6.5 Оценка качества переходного процесса по ЧХ

6.5.1 Оценка качества САУ по ее ВЧХ

основными признаками, которые позволяют судить о качестве САУ непосредственно по виду ВЧХ Р(ω), изображенных на рис. 6.5 являются следующие:

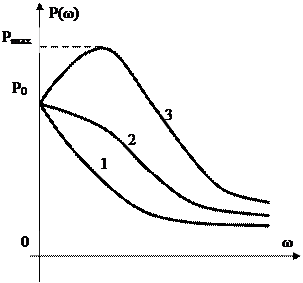Рисунок 6.5

1. Установившееся значение переходной характеристики равно начальному значению ВЧХ, т.е. 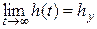= Р(0), где Р(0) – значение ВЧХ Р(ω) при ω=0. для астатических САУ h_у=р(0)=1, для статических h_у=р(0 = К/1+К.

2. Если ВЧХ Р(ω) представляет собой непрерывную положительную функцию частоты с отрицательной убывающей по абсолютной величине производной (рис. 6.5, кривая 1), т.е. Р(ω) > 0; dР(ω)/dω < 0, то переходная характеристика системы имеет монотонный характер, т.е. σ = 0 %.

3. Если ВЧХ Р(ω) есть непрерывная положительная невозрастающая функция частоты (рис. 5.6, кривая 2), т.е. если Р(ω) > 0; dР(ω)/dω ≤ 0, то переходная характеристика системы имеет перерегулирование σ ≤ 18 %.

4. Если непрерывная положительная ВЧХ Р(ω) имеет максимум (рис. 6.5, кривая 3), то переходная характеристика системы имеет перерегулирование

< %

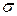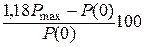5. Если ВЧХ Р(ω) имеет положительный Р _махи отрицательный Р _мin экстремумы (рис. 6.6), то

<

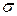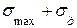
где 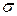< 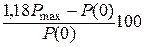%; σ_д = 0,3| Р _min | 100%

6. Длительность переходной характеристики (время t_р) в первом приближении оценивается шириной ВЧХ Р(ω), определяемой значением частоты ω_п, при которой Р(ω) < 0,1Р(0). Это значение частоты приближенно определяет полосу пропускания системы и называется интервалом положительности. Если ВЧХ Р(ω) имеет интервал положительности ω_п, то время регулирования t_р при ∆ = 0,05h_у в общем случае будет больше, чем π/ω_п, т.е. t_р > π/ω_п. для ВЧХ Р(ω) в виде кривой 1 на рис. 6.5 t_р > 4π/ω_п, а для ВЧХ в виде кривой 2 на рис. 6.5 t_р = (1-4)π/ω_п, т.е. π/ω_п ≤ t_р ≤ 4π/ω_п. для ВЧХ Р(ω) в виде кривой 3 на рис. 6.5 и для ВЧХ на рис. 6.6 время регулирования t_р тоже связано с ω_п обратно пропорциональной зависимостью, аналогичной (6.28). однако значение коэффициента пропорциональности (1-4) в этом случае зависит от Р _мах, увеличиваясь с возрастанием величины Р _мах.

Оценка качества переходного процесса по ВЧХ Р(ω) в значительной степени упрощается, если имеется связь между показателями качества и параметрами ВЧХ Р(ω). Такая связь в виде графических зависимостей σ и t_р от параметров ВЧХ Р(ω) была получена В.В. Солодовниковым.

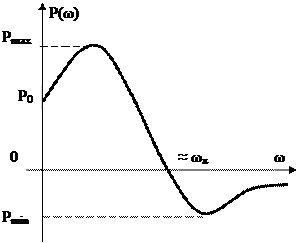Рисунок 6.6

На рис. 6.7 приведены наиболее часто встречающиеся три типовые формы ВЧХ. Условимся их называть ВЧХ первого типа (рис. 6.7а), ВЧХ второго типа (рис. 6.7б) и ВЧХ третьего типа (рис. 6.7в), положительная часть которой по форме может соответствовать одной из ВЧХ Р(ω) первого или второго типа.

Рассмотрим связь между показателями качества переходного процесса и ВЧХ второго типа, как наиболее часто встречающуюся на практике.

Аппроксимированная ВЧХ второго типа (рис. 6.7б) определяется, в основном, начальной ординатой Р (0), максимальным значением ВЧХ Р _мах, интервалом положительности ω_п и основным коэффициентом наклона = ω_d/ω_п. можно показать, что в системах с ВЧХ второго типа перерегулирование σ и время регулирования t_р = nπ/ω_п зависят от Р _мах и .

Строя переходные характеристики h(t) при заданном Р _мах для различного коэффициента 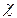, можно определить максимально возможные значения времени регулирования t_р и перерегулирования σ. Повторяя аналогичные построения h(t) для этого же параметра при других заданных значениях Р _мах, нетрудно получить данные для построения графиков зависимостей σ _мах = f ₁ (Р _мах) и t _{р мах} = f ₂ (Р _мах). Такие графики были построены В.В. Солодовниковым и для значений параметров < 0,8 изображены на рис. 6.8.

Из графиков видно, что при изменении Р _мах от 1,1 до 1,5 максимально возможное перерегулирование увеличивается от 22% до 42%. При этом увеличивается и максимально возможное время регулирование от 3,4 π/ω_п до

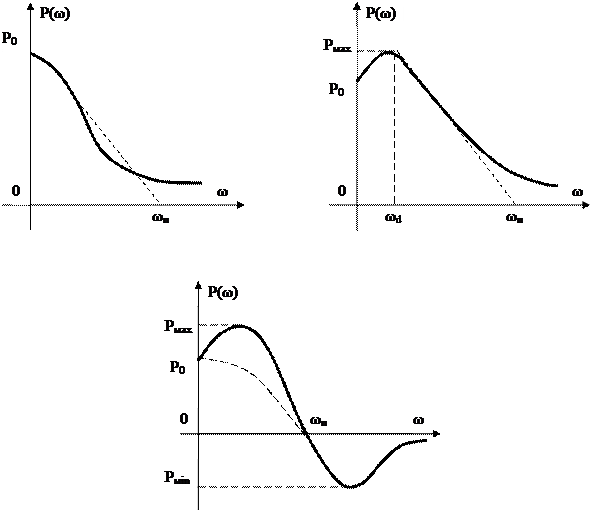Рисунок 6.7

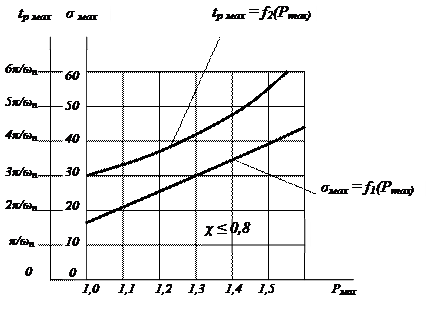Рисунок 6.8

6,7 π/ω_п. графики позволяют определить максимально возможные величины σ _мах и t_{р мах}, если известны параметры аппроксимированной ВЧХ второго типа.

Пример 1. Пусть исследуемая САУ имеет ВЧХ второго типа с параметрами Р (0) = 1, Р _мах = 1,25, ω_d = 9 с^-1, ω_п = 12 с^-1. требуется определить σ _мах и t_{р мах}.

решение. В данном примере = 9/12 = 0,75, т.е. значение второго параметра удовлетворяет неравенству ≤ 0,8. входя в графики по величине Р _мах = 1,25, получим σ _мах = 28%, t_{р мах} = 4,35 π/ω_п = 4,35*3,14/12 = 1,14 с.

Перейдем теперь к рассмотрению связи между показателями качества переходного процесса и параметрами ВЧХ Р(ω) третьего типа (рис. 6.7в). форма положительной части ВЧХ третьего типа может быть аналогична форме одной из ВЧХ первого или второго типа. Как показал анализ кривых h(t), соответствующих ВЧХ с различными Р _min при одних и тех же Р _мах и ω_п, время регулирования остается практически неизменным. Оно, в основном, определяется положительной частью ВЧХ. Поэтому при положительной части, соответствующей ВЧХ второго типа, время регулирования по-прежнему определяется по графикам, изображенным на рис. 6.8. установлено, что наличие отрицательного экстремума Р _min вызывает дополнительное перерегулирование σ _д, которое приближенно определяется выражением

σ_д ≈ 0,3| Р _min | 100% (6.29)

Следовательно, результирующее перерегулирование σ будет определяться соотношением

≤

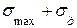
где σ _мах – перерегулирование, соответствующее положительной ВЧХ.

Пример 2. Пусть исследуемая САУ имеет ВЧХ Р(ω) третьего типа с параметрами Р (0) = 1, Р _мах = 1,2, Р _min = -0,3, ω_d = 4,8 с^-1, ω_п = 7 с^-1. = ω_d/ ω_п = 4,8/7 = 0,685 < 0,8. требуется определить время регулирования и перерегулирования.

Решение. По графикам для Р _мах = 1,2 имеем t_{р мах} = 4 π/ω_п = 4*3,14/7 = 1,79 с; σ _мах = 26%. В соответствии с выражением (6.29) и (6.30) получаем σ _д = 0,3*|-0,3|*100% = 9%; σ ≤ 26% + 9% = 35%. Это значит, что в исследуемой САУ с такой ВЧХ Р(ω) t_р ≤ 1,79 с; σ ≤ 35%.

Из изложенного следует, что графики (см. рис. 6.8) позволяют достаточно просто определять значения показателей качества переходного процесса t_р и σ системы по некоторым параметрам ее ВЧХ Р(ω), т.е. решать одну из важных задач анализа САУ. С другой стороны, эти графики можно использовать и для решения обратной задачи – задачи выбора по заданным значениям t_{р мах} и σ _мах некоторых параметров ВЧХ Р(ω) и ТЧХ L(ω), Θ(ω), поскольку между ВЧХ и ЛЧХ существует однозначная связь.

6.5.2 Оценка качества САУ по ее АЧХ А( ω)

если САУ минимально-фазовая, то качество можно оценить по одной АЧХ А(ω). В большинстве реальных САУ АЧХ А(ω) имеет вид, изображенный на рис. 6.9.

По АЧХ можно приближенно оценить колебательность и быстродействие системы.

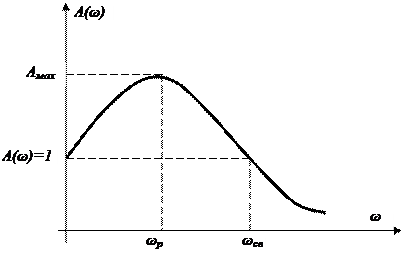Рисунок 6.9

Колебательность системы определяется по величине показателя колебательности М, представляющего собой отношение максимального значения АЧХ А_мах замкнутой САУ к ее значению при ω = 0, т.е. М = А_мах/А(0). Для астатических САУ М = А_мах, так как А(0) = Р(0) = 1. Для статических САУ А(0) = Р(0) = К/(1+К), причем, если К ≥ 1, то в этом случае М ≈ А_мах. Поэтому часто показателем колебательности называют величину М = А_мах = |Ф(jω)|_мах. Чем больше М = А_мах, тем меньше запас устойчивости и тем более колебательный переходный процесс. При М → ∞ колебательность возрастает до получения незатухающих колебаний, соответствующих нахождению системы на границе устойчивости. Примером такой связи колебательности переходного процесса с максимумом АЧХ может служить колебательное звено. Большое число расчетов и экспериментов показало, что в хорошо демпфированных системах показатель колебательности не должен превышать значений М = 1,1-1,5, хотя иногда он может достигать М = 2-2,5. при М > 2 имеет место чрезмерная колебательность переходной составляющей процесса управления.

Для оценки быстродействия системы может использоваться резонансная частота ω_р, соответствующая максимальной ординате АЧХ, и во многих случаях близкая к частоте среза замкнутой системы ω_сз (см. рис. 6.9). так как частота колебаний переходной характеристики ω_к = 2πf_к примерно равна ω_р(ω_сз), то время достижения первого максимума переходной характеристикой равно примерно половине периода колебаний этой частоты, т.е t_m ≈ π/ω_р ≈ π/ω_сз. Если при этом предположим, что переходная характеристика системы в течение t_р имеет 1-2 колебания, то

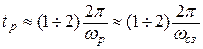
Таким образом, показатель колебательности М = А_мах и характерные частоты ω_р, ω_сз замкнутой САУ так же, как Р_мах и , ω_п являются косвенными показателями качества переходного процесса.

В заключение заметим, что амплитудно-частотные характеристики А(ω) устойчивых систем по своему виду подобны АЧХ колебательного звена. Поэтому, если показатель колебательности М > 1, то замкнутую САУ можно аппроксимировать колебательным звеном, т.е. считать, что

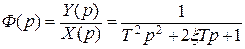
Тогда

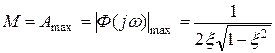
График М = f(ξ), соответствующий выражению (6.33), приведен на рис. 6.10а.

Для передаточной функции (6.31) на основе графиков h(t) можно установить зависимость перерегулирования σ и времени регулирования t_р от относительного коэффициента затухания ξ. Эти зависимости в виде кривых σ = f₁(ξ), t_р = f₂(ξ) изображены на рис. 6.10б. воспользовавшись графиками М = f(ξ) и σ = f₁(ξ) нетрудно найти зависимость перерегулирования σ от показателя колебательности М. эта зависимость представлена на рис. 6.10в.

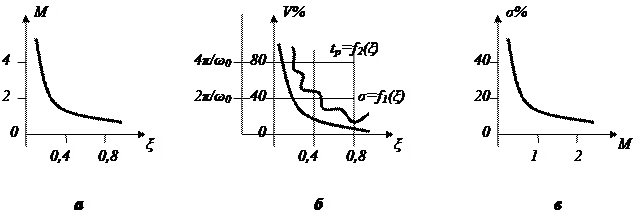
Рисунок 6.10

Следовательно, для приближенной оценки показателей качества переходного процесса систем, АЧХ А(ω) которых близки к АЧХ колебательного звена, необходимо: а) по графику АЧХ А(ω) определить значение М и ω_р; б) войти по значению М в график рис. 6.10а и найти ξ; в) по значению ξ войти в график рис. 6.10б и определить искомые показатели σ в процентах % и t_р в nπ/ω_о, где ω_о=1/Т_о – собственная частота колебаний, определяемая по формуле ω_о=ω_р/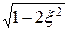, которая вытекает из выражения ω_р=ω_о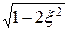. заметим также, что перерегулирование может быть найдено и по показателю колебательности М из графика 6.10в.

6.5.3 Оценка качества САУ по частотным

характеристикам разомкнутой системы

основными частотными характеристиками разомкнутой системы по которым можно приближенно оценить качество переходного процесса замкнутой САУ, является АФХ W(jω) и ЛЧХ L(ω), Θ(ω). Так, например, по АФХ W(jω) и по ЛЧХ L(ω), Θ(ω) можно определить запасы устойчивости системы по амплитуде (модулю) и фазе. В хорошо демпфированных системах запас устойчивости по амплитуде должен составлять 6-20 дБ, что соответствует 2-10 в линейном масштабе, а по фазе 30-60⁰. чем меньше запасы устойчивости Θ_з и L_з, тем больше склонность системы к колебаниям и тем выше резонансный пик А_мах, т.е. тем больше показатель колебательности М.

С помощью АФХ W(jω) и ЛЧХ L(ω), Θ(ω) можно определить не только запасы устойчивости системы по амплитуде и фазе, но и показатель колебательности М, резонансную частоту ω_р и другие числовые характеристики, являющиеся важными критериями качества САУ.

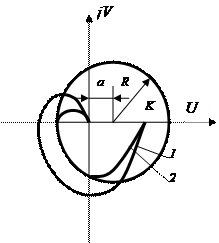
Наиболее простой оценкой колебательности переходной характеристики h(t) замкнутой САУ по ее АФХ W(jω) в разомкнутом состоянии является признак колебательности. Суть этого признака состоит в следующем. Если АФХ W(jω) астатической системы (кривая 1 на рис. 6.11а) пересекает прямую U = -0,5, то переходная характеристика – колебательная. Если пересечения нет (кривая 2 на рис. 6.11а), то переходная характеристика имеет монотонный характер. Если АФХ статической системы (кривая 1 на рис. 6.11б) пересекает окружность радиуса , центр которой расположен на положительной вещественной полуоси в точке 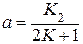, где К - коэффициент передачи разомкнутой системы, то переходная характеристика – колебательная. При отсутствии указанного пересечения (кривая 2 на рис. 6.11 б) переходная характеристика имеет монотонный характер.

		a		б

Рисунок 6.11

В инженерной практике наиболее широкое применение получила оценка качества замкнутой САУ по виду ее ЛЧХ L(ω), Θ(ω) в разомкнутом состоянии, основанная на связи параметров ЛЧХ с параметрами ВЧХ. Причем, если система в разомкнутом состоянии минимально-фазовая, то о качестве САУ можно судить только по одной амплитудной характеристике (по асимптотической ЛАХ). На основании расчетов переходных характеристик h(t) установлено, что для удовлетворительного качества САУ ЛАХ в окрестности частоты среза ω_с должна иметь наклон -20 дБ/дек. Протяженность этого участка влияет на перерегулирование. В частности, с увеличением этого участка уменьшается перерегулирование и, следовательно, число колебаний в переходном процессе. Время регулирования зависит от частоты среза ω_с; чем больше ω_с, тем меньше t_р. В связи с возможностью такой оценки качества управления введены типовые ЛАХ L(ω) для САУ с астатизмом первого порядка (рис. 6.12). при этом ЛАХ условно разделяют на три основные участка: низкочастотный, среднечастотный и высокочастотный.

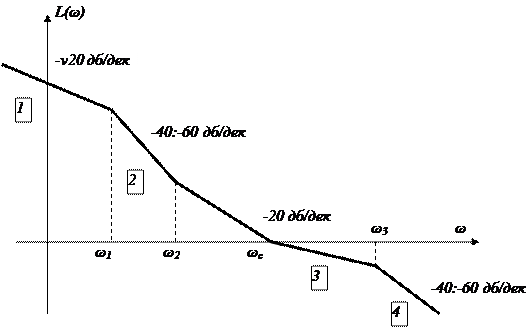Рисунок 6.12

Низкочастотный участок ЛАХ (0, ω) характеризует точность системы в установившемся режиме, так как его вид всецело определяется количеством интегрирующих звеньев ν и коэффициентов передачи К. наклон этого участка составляет - ν ·20 дБ/дек, где ν – порядок астатизма системы относительно задающего воздействия. Напомним, что при ν = 0 система является статической; при ν = 1 –астатической первого порядка; при ν = 2 – астатической второго порядка и т.д.

Среднечастотный участок (ω₂, ω₃) определяет запас устойчивости системы и в значительной мере форму переходной характеристики h(t). ЛАХ вблизи частоты среза ω_с должна иметь наклон - 20 дБ/дек, а протяженность этого участка не должна быть меньше декады, т.е. ω₃/ω₂ ≥ 10, и отношение частот 2 ≤ ω₃/ω_с ≤ 4. эти неравенства определяют не только длину среднечастотного участка ЛАХ с наклоном -20 дБ/дек, но и положение частоты среза на этом участке. При выполнении указанных неравенств замкнутая САУ будет иметь необходимые запасы устойчивости Θ_з, L_з и практически приемлемые значения перерегулирования σ и времени регулирования t_р. Например, САУ с ЛАХ наклоны участков 1, 2, 3 и 4 которой равны -20 дБ/дек, -40 дБ/дек, -20 дБ/дек, -40 дБ/дек., будет иметь σ ≤ 20-30%, t_р ≈ π/ω_с, если ω₂/ω₃ ≈ 10; 2 < ω₃/ω_с < 4; при ω₃/ω₂ < 10 переходная характеристика этой САУ имеет излишне колебательный характер.

Высокочастотный участок (ω, ∞) не оказывает существенного влияния на качество системы. Он включает интервал частот, в котором L(ω) < -16 дБ, что соответствует Р(ω) ≤ (0,1-0,2)Р(0). Влияние этой высокочастотной области сказывается на начальном участке переходной характеристики.

Участок ЛАХ в интервале частот от ω₁ до ω₂ можно считать промежуточным. Он оказывает менее существенное влияние на точность системы и показатели качества h(t), чем низкочастотный и среднечастотный участки.

Промежуточный и высокочастотный участки типовой ЛАХ обычно имеют наклон (-40, -60 дБ/дек). Поэтому различают четыре типа ЛАХ, участки 1, 2, 3 и 4, которых имеют соответственно следующие наклоны в дБ/дек: ЛАХ 1 типа: -20, -40, -20, -40; ЛАХ 2 типа: -20, -60, -20, -40; ЛАХ 3 типа: -20, -40, -20, -60; ЛАХ 4 типа: -20, -60, -20, -60.

Для типовых ЛАХ составлены специальные номограммы качества, по которым, располагая параметрами типовых ЛАХ, можно найти основные показатели качества переходного процесса h(t), а также получить дополнительные сведения о качестве САУ. В практике используются номограммы качества В.В. Солодовникова и г.Честната, Р.Майера. при разработке этих номограмм за основные параметры типовых ЛАХ были приняты: а) L(ω₁) – ордината ЛАХ при частоте ω₁; б) ω₁/ω_с, ω₃/ω_с – отношение частот ω₁ и ω₃ к частоте среза; в) наклон промежуточного и высокочастотного участков.

Номограммы качества Солодовникова позволяют по перечисленным параметрам типовых ЛАХ найти время регулирования t_р, перерегулирования σ, максимальное значение второй производной переходной характеристики, запас устойчивости системы по фазе Θ_з, а также коэффициенты ошибок с₁, с₂. номограммы качества Честната-Майера по тем же параметрам ЛАХ дают возможность определить время регулирования t_р, время t_м – достижения максимума переходной характеристики, величину максимума h_мах, круговую частоту колебаний переходной характеристики, а также величину максимума А_мах АЧХ А(ω) на резонансной частоте ω_р. Полное описание этих номограмм и их применение для определения перечисленных показателей качества по типовым ЛАХ астатических систем первого порядка и по ЛАХ, близким к типовым, можно найти в литературе по ТАУ.

Следует иметь в виду, что эти номограммы качества могут быть использованы и при исследовании статических систем, а также систем с астатизмом выше первого порядка для определения перерегулирования и времени регулирования t_р. Объясняется это тем, что если две ЛАХ, соответствующие минимально-фазовым системам, отличается друг от друга лишь в области низких частот, где | W(jω) | = Н(ω) ≥ 1, то им соответствуют близкие ВЧХ, а следовательно, и переходные характеристики h(t). Так, например, если ЛАХ L(ω) статической системы и системы с астатизмом первого и второго порядка совпадают при тех ω, при которых | L(ω) | > 30 дБ, то ВЧХ Р(ω) этих систем в замкнутом состоянии отличаются от ВЧХ системы с астатизмом первого порядка не более чем на 2,5%.