Передаточные функции системы

Будем полагать, что процессы, проходящие в САР, описываются линейными дифференциальными уравнениями с постоянными коэффициентами. Таким образом, мы ограничимся рассмотрением линейных САР с постоянными параметрами, т.е. параметрами, не зависящими ни от времени, ни от состояния системы.

Пусть для динамической системы (см. рис.)

дифференциальное уравнение записано в операторной форме

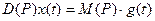(1)

где D(P) и M(P) – многочлены от P.

,

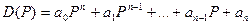(2)

,

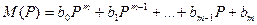P – оператор дифференцирования;

x(t) – выходная координата системы;

g(t) – входное воздействие.

Преобразуем (1) по Лапласу, предположив нулевые начальные условия.

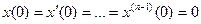
Введем обозначения

; ,

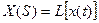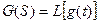получим, учитывая, что

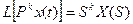
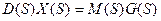, (3)

где

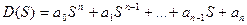
(4)

Используем обозначение

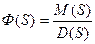, (5)

тогда уравнение (3) примет вид:

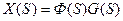. (6)

Уравнение (6) связывает изображение Х (S) выходной координаты системы с изображением G(S) входного воздействия. Функция Ф(S) характеризует динамические свойства системы. Как следует из (4) и (5), эта функция не зависит от воздействия, приложенного к системе, а зависит лишь от параметров системы. Учитывая (6) функцию Ф(S) можно записать следующим образом

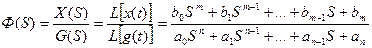(7)

Функция Ф(S) называется передаточной функцией системы. Из (7) видно, что передаточная функция представляет собой отношение изображения по Лапласу входной координаты системы к изображению по Лапласу входного воздействия при нулевых начальных условиях.

Зная передаточную функцию системы Ф(S) определив изображение G(S) воздействия g(t), приложенного к системе можно найти по (6) изображение Х(S) выходной координаты системы х (t), затем, переходя от изображения Х(S) к оригиналу х(t) получить процесс изменения выходной координаты системы при приложении к этой системе входного воздействия.

Многочлен в знаменателе передаточной функции, называется характеристическим полиномом, а уравнение

D(S) =0 (8)

характеристическим уравнением.

Для системы, описываемой уравнением n-го порядка, характеристическое уравнение представляет собой алгебраическое уравнение n-ой степени и имеет n корней, S₁ S_2…S_n, среди которых могут быть как вещественные, так и комплексно – сопряженные.

Корень многочлена стоящего в знаменателе передаточной функции называются полюсами этой передаточной функции, а в числителе – нулями.

Представим многочлены в виде:

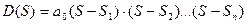(9)

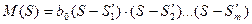(10)

Поэтому передаточная функция

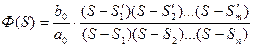. (11)

Отсюда следует, что задание нулей и полюсов определяет передаточную функцию с точностью до постоянного множителя .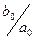

В том случае, когда вещественные части всех полюсов передаточной функции отрицательны, т.е.

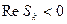, k=1,2…n,система называется устойчивой. В ней переходная составляющая выходной величины (собственного движения) с течением времени затухает.