При описании динамики экономических явлений мы сравнивали изменения результата 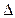 у (х) с величиной приложенных усилий
у (х) с величиной приложенных усилий 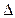 х, т.е. изучали отношение
х, т.е. изучали отношение 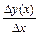 - среднюю эффективность усилий; и переходя к пределу при
- среднюю эффективность усилий; и переходя к пределу при 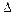 х
х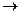 0 этого отношения, получали предельную эффективность на уровне усилий х.
0 этого отношения, получали предельную эффективность на уровне усилий х.
В некоторых экономических задачах необходимо проводить аналогичные сравнения не для абсолютных приращений 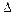 х и
х и 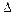 у, а для относительных приращений
у, а для относительных приращений 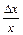 и
и 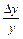 (безразмерных величин).
(безразмерных величин).
Эластичностью Ex (y) функции у называется предел отношения относительного приращения функции у к относительному приращению переменной х при 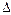 х
х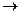 0,
0, 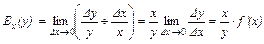 ,
, 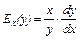 .
.
Эластичность функции показывает, на сколько процентов изменится функция у = f (х) при изменении независимой переменной х на 1%.
Геометрический смысл эластичности функции По определению эластичности имеем 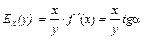 , где
, где 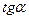 - тангенс угла наклона касательной, проведенной к графику функции у=f (х) в точке М (х; у).
- тангенс угла наклона касательной, проведенной к графику функции у=f (х) в точке М (х; у).
Если f (x) – возрастает на промежутке Х, то из 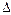 АВМ имеем: у = АВ АВМ имеем: у = АВ 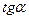 , тогда , тогда 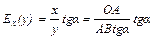 , ,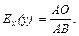 Т.о., эластичность функции f(х) в точке М равна отношению ОА к Т.о., эластичность функции f(х) в точке М равна отношению ОА к | 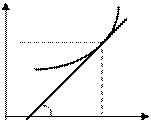 у=f (х) у М (х; у) у В a А 0 х у=f (х) у М (х; у) у В a А 0 х | Если f (x) убывает на промежутке Х, то из  АВМ имеем АМ = у = АВ АВМ имеем АМ = у = АВ 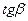 =- =- , , 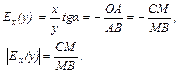 |  у=f (х) С у М (х; у) у А b a 0 х В у=f (х) С у М (х; у) у А b a 0 х В |
ВА - проекции касательной в точке М на ось ОХ. Если абсцисса точки B >0, то АВ < АО и 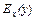 >1, если абсцисса точки B <0, то АВ > АО и >1, если абсцисса точки B <0, то АВ > АО и 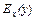 <1. <1. | Eсли СМ > МВ, то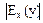 >1; если СМ < МВ, то >1; если СМ < МВ, то 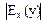 <1. Замечание для убывающей функции <1. Замечание для убывающей функции  )<0. )<0. |
Если 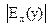 >1, то тенденцию, описывающую функцией у читают эластичной,
>1, то тенденцию, описывающую функцией у читают эластичной, 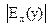 <1 – неэластичной.
<1 – неэластичной.
Свойства эластичности функции (ЭФ)
10. ЭФ – безразмерная величина, не зависящая от единиц измерения х и у.
20. ЭФ – зависит от величины аргумента х, т.е. является функцией переменной х.
30. Эластичность произведения (частного) двух функций равна сумме (разности) эластичностей этих функций 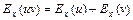 ,
, 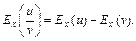
40. Эластичности взаимно-обратных функций взаимно-обратны 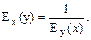
50. ЭФ равна произведению независимой переменной х на темп роста функции 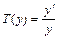 , т.е.
, т.е. 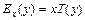 .
.
 2014-02-09
2014-02-09 1789
1789
