2014-02-24
643
На рис.4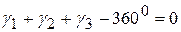 
. Если γ’i - углы, вычисленные по измеренным сторонам, (γi) – поправки к ним из уравнивания сети, то
.
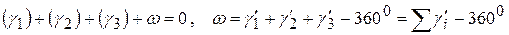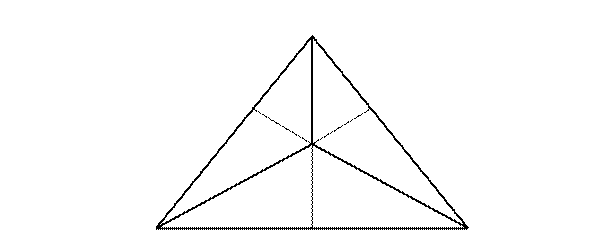
Рис.4
Используя для определения поправок (γi) формулы (5), после преобразований находим
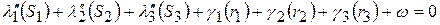, (7)
где
.
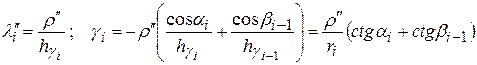В рассматриваемом случае n = 3;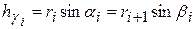 
.
Условия дирекционных углов возникают при избыточных дирекционных углах линий. В угловой форме (рис.5)
.
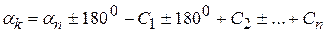Рис.5
Если С’i - углы, вычисленные по измеренным сторонам, (Сi) – поправки к ним из уравнивания сети, то
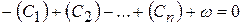, (8)
где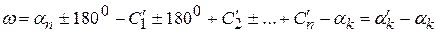 
.
Заменив поправки в углы на поправки в стороны и учитывая, что поправки (bн) и (bк) в исходные стороны bн и bк равны нулю, имеем
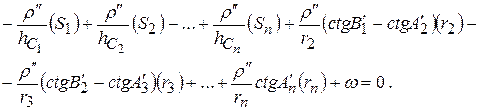(9)
Базисные условия в сетях трилатерации не возникают.
Условия координат (абсцисс и ординат) возникают в тех же случаях, что и в триангуляции. Сначала координатные условия записывают в угловой форме (как в триангуляции при уравнивании углов), а затем поправки углов выражают через поправки к длинам сторон.
