Def 1. Плоскость, проходящая через касательную к кривой в т. 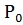 и ортогональная соприкасающейся плоскости, называется спрямляющей плоскостью.
и ортогональная соприкасающейся плоскости, называется спрямляющей плоскостью.
Def 2. Бинормалью называется прямая, которая получается при пересечении спрямляющей плоскости нормальной плоскостью.
Замечание. Из определений следует, что вектор бинормали 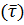 - ортогонален касательному вектору (т.к. спрямляющая плоскость перпендикулярна касательной) и вектору главной нормали (т.к. вектор главной нормали принадлежит соприкасающейся плоскости), т.е.
- ортогонален касательному вектору (т.к. спрямляющая плоскость перпендикулярна касательной) и вектору главной нормали (т.к. вектор главной нормали принадлежит соприкасающейся плоскости), т.е. 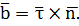
| B |
 |
| r |
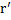 |
| R |
 |
Вектор 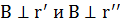 (т.к. в
(т.к. в  соприкасающейся плоскости)
соприкасающейся плоскости) 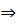
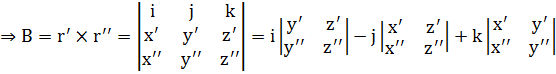
Теперь можем записать уравнение бинормали в каноническом виде:
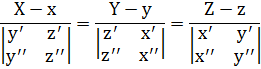
или
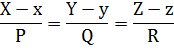
Уравнение главной нормали
В качестве направляющего вектора главной нормали можно выбрать вектор равный 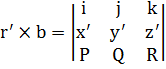 , тогда получим следующее уравнение:
, тогда получим следующее уравнение:
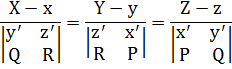
Уравнение спрямляющей плоскости
Для спрямляющей плоскости вектором нормали является направляющий вектор главной нормали, поэтому получим следующее уравнение:
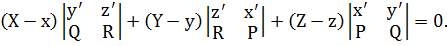
| b |
| n |
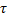 |
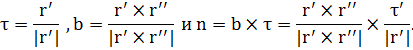
 2015-04-12
2015-04-12 11452
11452








