Полиномы Лежандра Ln (x) отрогональны на отрезке [–1, 1] с единичной весовой функцией h (x)=1. Они могут быть определены на основе рекурентного соотношения
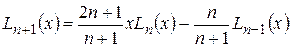 , (2.3)
, (2.3)
при этом L 0(x)=1, L 1(x)= x.
Нормирующий множитель (квадрат нормы)
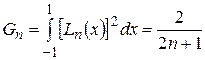 .
.
На рисунке 2.1 показаны первые четыре полинома Лежандра, вычисленные на основе (3). Упорядочение осуществляется по степени полинома.
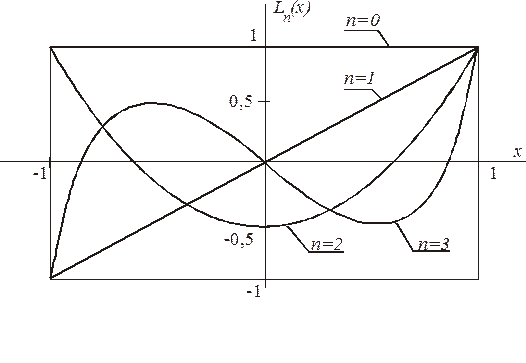
Рисунок 2.1 – Полиномы Лежандра
Вычисление спектральных коэффициентов производится по формуле, аналогичной формуле (1.6) из темы 1:
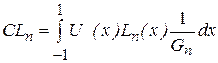 . (2.4)
. (2.4)
Если сигнал, подлежащий исследованию, представлен в виде дискретных во времени отсчетов, то целесообразно использовать дискретные полиномы Лежандра. Аргументом при этом является последовательность натуральных чисел 0, 1, 2,…, k,…, Km, где Km – номер последнего отсчета.
В общем виде дискретный полином Лежандра степени n определяется на Кm +1 равноотстоящих отсчетов выражением
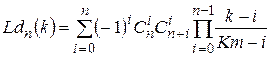 , (2.5)
, (2.5)
где 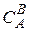 – число сочетаний из А элементов по В элементов, n =0, 1, 2, ….
– число сочетаний из А элементов по В элементов, n =0, 1, 2, ….
Полиномы (2.5) ортогональны на отрезке [0, Km ] с единичной весовой функцией.
Нормирующий множитель (квадрат нормы) определяется как
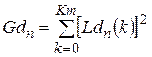 . (2.6)
. (2.6)
Спектральные коэффициенты определяются в этом случае выражением
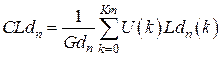 . (2.7)
. (2.7)
 2014-02-24
2014-02-24 1980
1980








