Спектральное представление периодических сигналов. Базисные функции

Рассмотренные модели сигналов в виде функций времени предназначены в первую очередь для анализа формы сигнала. Реальные сигналы часто имеют достаточно сложную форму (например сигнал ЭКГ). При исследовании прохождения таких сигналов через радиоэлектронные устройства желательно было бы иметь такое представление сигналов, которое упростило бы это исследование. Для этого сигнал сложной формы удобно представить в виде совокупности каких-то элементарных сигналов. На практике наибольшее применение нашло представление непрерывного сигнала сложной формы u(t), заданного на интервале (t₁,t₁+T), где Т – период повторения сигнала, в виде линейной комбинации некоторых элементарных функций j_k(t), k=0, 1, 2, …

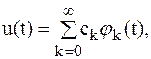t₁ £ t £ t₁+T, (1.1)

где с_k – некоторый безразмерный коэффициент,

k – порядковый номер функции в системе {j_k(t)}.

Функции j_k(t) называют базисными. При выбранном наборе базисных функций сигнал u(t) полностью определяется совокупностью коэффициентов c _k.

Совокупность коэффициентов c_k называют дискретным спектром сигнала, а представление сигнала в виде (1.1) называют обобщенным спектральным представлением или разложением сигнала по системе базисных функций {j_k(t)}.

Такое представление сигнала удобно для изучения линейных систем. Оно позволяет находить реакцию системы, т. е. сигнал на ее выходе, на любой сложный входной сигнал. Для этого определяют реакцию на каждое элементарное воздействие, полученные результаты умножают на коэффициенты c _k и суммируют, поскольку линейные системы удовлетворяют принципу суперпозиции.

Требования к базисным функциям:

- для любого сигнала ряд (1.1) должен сходиться,

- коэффициенты c _k должны легко вычисляться,

- значения коэффициентов c _k не должны зависеть от верхнего предела суммы (1.1).

Указанным требованиям удовлетворяет так называемая полная, упорядоченная система линейно независимых функций.

Система функций j_k(t), k=0, 1, 2, …, N-1, называется линейно независимой, если равенство

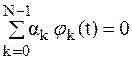(1.2) справедливо лишь при a_k=0 для всех k. Это значит, что никакую функцию этой системы нельзя представить в виде линейной комбинации других функций этой же системы.

Упорядоченность означает, что всегда по некоторому признаку можно определить, какая функция является предыдущей, а какая – последующей.

Система линейно независимых функций является полной, если к ней нельзя добавить ни одной новой функции, которая была бы линейно независимой по отношению к функциям рассматриваемой системы.

Если система окажется неполной, то не все сигналы можно представить в виде (1.1). Например, если мы разложим сигнал по первым 5 гармоникам, то мы не сможем узнать о наличии в сигнале более высокочастотных гармоник.

Неполную систему всегда можно дополнить введением новых функций. В пределе можно получить полную систему.

Коэффициенты ряда (1.1) просто вычисляются, если в качестве базиса использовать систему ортогональных функций.

В общем случае функции j_k(t), k=0, 1, 2, …, заданные на интервале t₁ £ t £ t₁+T, называют ортогональными на этом интервале, если выполняется условие

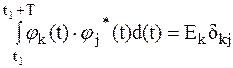, (1.3)

где d_kj – символ Кронекера, равный 1 при k=j и 0 при k¹j,

* - символ комплексной сопряженности.

Постоянная E_k физически соответствует энергии сигнала j_k(t). Величину 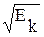называют нормой базисной функции j_k(t).

Для действительных функций j_k(t), k=0, 1, 2,… условие ортогональности имеет вид

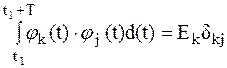. (1.4)

Система ортогональных функций является частным случаем системы линейно независимых функций.

На практике часто пользуются ортонормированной системой функций {y_k(t)}, которая образуется из системы ортогональных функций {j_k(t)} нормировкой каждой функции по ее норме, т. е. делением на норму

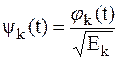
. (1.5)

Вычисление спектральных коэффициентов

Коэффициенты ряда (1.1) находятся следующим образом. Умножим обе части равенства (1) на j_j^*(t) и проинтегрируем на интервале (t₁, t₁+T)

.

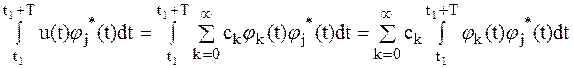С учетом выражения (3) получим

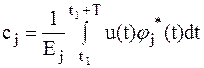, j=0, 1, 2, … (1.6)

При использовании ортонормированной системы

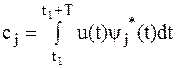, j=0, 1, 2, … (1.7)

Представление сигнала в виде (1.1) называют обобщенным спектром Фурье. Коэффициенты c_j, определяемые (1.6) или(1.7), называют обобщенными коэффициентами Фурье. Совокупность коэффициентов c_j и порядковых номеров функций называют обобщенным спектром сигнала.

Тема 2. Системы базисных функций, применяемые при обработке биомедицинских сигналов: система тригонометрических функций; система комплексных экспоненциальных функций; полиномы Лежандра; функции Уолша; функции Хаара.