Спектр непериодического сигнала

В предыдущей теме были получены выражения для определения комплексных спектральных коэффициентов разложения периодического сигнала u (t) в базисе комплексных экспоненциальных функций

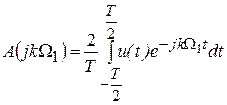(3.12)

и представления этого сигнала совокупностью спектральных коэффициентов

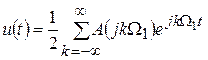. (3.13)

Используем эти выражения для определения спектра непериодического сигнала. Подставим значения спектральных коэффициентов из (3.12) в (3.13)

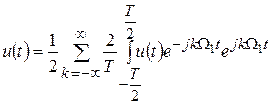. (4.1)

Переход от периодического сигнала к непериодическому можно осуществить следующим образом. При неограниченном увеличении периода 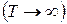периодический сигнал переходит в одиночный сигнал, определенный на интервале существования от t ₁ до t ₂, то есть в непериодический сигнал.

Как при этом будет изменяться спектр сигнала? По мере увеличения периода Т спектральные составляющие сближаются, в пределе 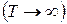до полного слияния. Таким образом, спектр непериодического сигнала является сплошным. Амплитуда каждой спектральной составляющей по мере увеличения Т уменьшается, стремясь в пределе 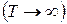к нулю.

Что изменится в выражении (4.1) при неограниченном увеличении периода Т? Учтем, что Т и Ω₁ связаны соотношением 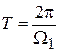или .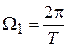

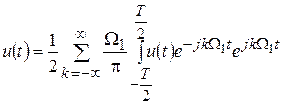. (4.1а)

Частота первой гармоники Ω₁ в пределе стремится к нулю, то есть можно считать, что справедливо преобразование 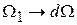. При этом частоты спектральных составляющих k Ω₁ преобразуются в текущую частоту Ω. Исходя из этого, суммирование в (4.1а) можно заменить интегрированием по частоте и выражение (4.1а) представить в виде

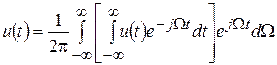. (4.2)

Внутренний интеграл в выражении (4.2) (он выделен квадратными скобками) называют спектральной характеристикой непериодического сигнала u (t)

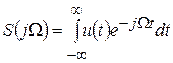. (4.3)

Выражение (4.3) называют прямым интегральным преобразованием Фурье.

Непериодический сигнал u (t) может быть представлен его спектральной характеристикой S (j Ω) с помощью обратного интегрального преобразования Фурье

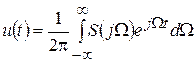. (4.4)