Как изменится спектр сигнала при его преобразовании из непрерывной формы в дискретную? Спектр непрерывного одиночного сигнала (рисунок 10.1, верхний ряд, слева) является сплошным (рисунок 10.1, верхний ряд, справа).
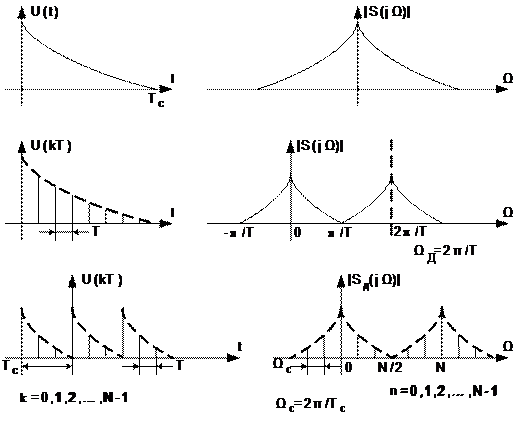
от непрерывного сигнала к дискретному
Спектр дискретного сигнала (рисунок 10.1, средний ряд, слева) становится периодическим, и период повторения спектральных составляющих определяется периодом дискретизации Т (рисунок 10.1, средний ряд, справа).
Спектр дискретного сигнала имеет спектральные составляющие на частоте дискретизации. У каждой составляющей имеются также боковые составляющие, которые определяются спектром исходного непрерывного сигнала. На частотах 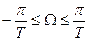 спектральная характеристика дискретного сигнала совпадает со спектральной характеристикой исходного непрерывного сигнала (рисунок 10.1, средний ряд).
спектральная характеристика дискретного сигнала совпадает со спектральной характеристикой исходного непрерывного сигнала (рисунок 10.1, средний ряд).
|
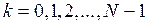 . Тогда длительность сигнала
. Тогда длительность сигнала 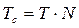 . Будем считать, что сигнал периодически повторяется с периодом
. Будем считать, что сигнал периодически повторяется с периодом 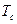 . Если дискретный сигнал периодически повторяется (рисунок 10.1, нижний ряд, слева), то его спектр становится периодическим и дискретным (рисунок 10.1, нижний ряд, справа).
. Если дискретный сигнал периодически повторяется (рисунок 10.1, нижний ряд, слева), то его спектр становится периодическим и дискретным (рисунок 10.1, нижний ряд, справа).
Длительность наблюдения сигнала, принимаемая за период повторения наблюдаемого сигнала, определяет разрешающую способность спектра этого сигнала по частоте в низкочастотной области и между соседними составляющими.
Число дискретных отсчетов, которыми представлен сигнал, наблюдаемый в течение времени Тс, определяет максимальную по частоте составляющую, которую можно обнаружить в спектре сигнала.
Для дискретных периодических сигналов преобразование сигнала из временной формы в частотную производится с помощью прямого дискретного преобразования Фурье, а преобразование из частотной формы во временную – с помощью обратного дискретного преобразования Фурье.
Переход от непрерывного к дискретному преобразованию Фурье осуществляется следующим образом. В базисных функциях 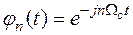 осуществляется замена:
осуществляется замена:
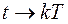 ;
; 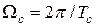 ;
; 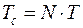 .
.
В результате n -я базисная функция дискретного аргумента k будет иметь вид
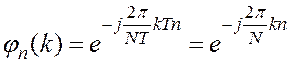 , (10.1)
, (10.1)
где 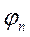 - дискретная базисная функция,
- дискретная базисная функция,
n – номер базисной функции,
роль времени выполняют порядковые номера отсчетов k,
роль периода выполняет число дискретных отсчетов N, умещающихся на одном периоде сигнала Тс.
Применяют следующие обозначения:
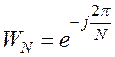 ; тогда
; тогда 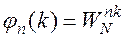 .
.
 2014-02-24
2014-02-24 1298
1298
