2014-02-24
597
Как и непрерывные базисные функции, функции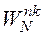 
ортогональны.
,
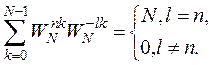N является квадратом нормы.
Функции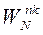 
являются периодическими с периодом N. Периодичность сохраняется как по n, так и по k. Аналитически это свойство представляется так:
.
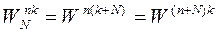С учетом введенных обозначений прямое дискретное преобразование Фурье (ПДПФ) запишется следующим образом
, 
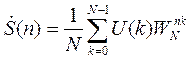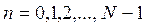, (10.2)
а обратное дискретное преобразование Фурье (ОДПФ):
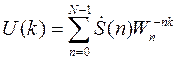. (10.3)
Спектр дискретного периодического сигнала также дискретный и периодический с периодом N:
, 
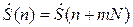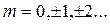
Это является особенностью дискретного преобразования Фурье.
Для расчета n -ой составляющей частотного спектра используют все N отсчетов сигнала во времени. Для определения одного отсчета во времени используют все N частотных составляющих.
Чем больше время наблюдения сигнала Т с, принимаемое за период его повторения, тем большее разрешение по частоте можно получить, так как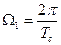 
. Чем большим числом отсчетов N представлен сигнал, тем более высокочастотные составляющие в спектре сигнала можно выявить.
