Правило проверки нулевой гипотезы

1) Вычислить теоретические частоты .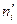

2) Рассчитать 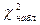по формуле (10.1).

3) По таблице критических точек 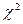найти .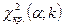

4) Если 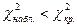- нет оснований отвергнуть нулевую гипотезу .

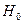Если 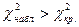- нулевую гипотезу 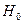отвергают.

Замечание. Объём выборки должен быть не менее 50 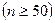. Каждый интервал должен содержать не менее 5 – 8 вариант. Малочисленные интервалы следует объединять с соседними, суммируя частоты.

Пример 10.1. Для заданного эмпирического распределения при уровне значимости 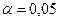проверить гипотезу о нормальном распределении.

Решение. Найдем выборочные среднюю и дисперсию

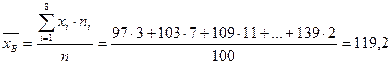
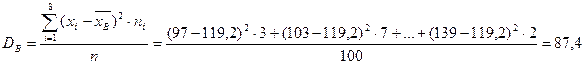
Выборочное среднеквадратическое отклонение .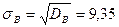

Составим формулу для вычисления теоретических частот

.

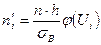
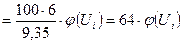Вычислим 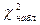, для чего составим таблицу.

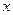
интервалы	Серед.
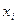
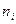
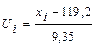
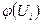
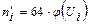
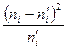
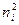
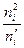
94-100		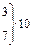	-2,37	0,0241		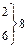0,5		12,5
100-106		-1,73	0,0893
106-112			-1,09	0,2203		0,64		8,64
112-118			-0,45	0,3605		0,39		17,39
118-124			0,19	0,3918		0,36		31,36
124-130			0,83	0,2827		0,06		20,06
130-136		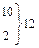	1,48	0,1334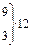
136-142		2,12	0,0422
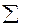
						1,95		101,95

Согласно замечанию частоты первых двух и последних двух интервалов суммируются.

Столбцы 8 и 9 служат для проверки правильности вычислений по формуле

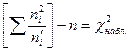
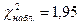(последняя ячейка 7 столбца)

Проверка: .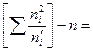

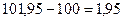Вычисления произведены правильно.

По таблице критических точек распределения 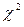(см. приложения учебников), по уровню значимости 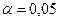и числу степеней свободы 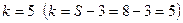находим .

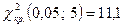Так как 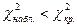- нет оснований отвергнуть нулевую гипотезу, то есть расхождения эмпирических и теоретических частот незначимо.

Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении совокупности.

Тема 11. Корреляция и регрессия

Пусть нам требуется установить и оценить зависимость между случайными величинами и . Они могут быть связаны либо функциональной зависимостью, либо статистической, либо быть независимыми.

Например, между радиусом круга 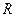и его площадью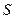существует функциональная зависимость 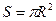. Однако на практике чаще всего встречаются зависимые друг от друга переменные величины, но при этом каждой из них не соответствует определённое значение другой. Например, связь между количеством осадков и урожайностью имеется. Однако известно, что количество осадков однозначно не определяет урожайность. Это объясняется тем, что на урожайность влияет много других факторов. В результате каждому значению одной величины соответствует несколько значений другой величины. Связи такого типа называются статистическими.

В частности, если при изменении одной из величин изменяется среднее значение другой, то такая зависимость называется корреляционной. Основная задача теории корреляции – выявление связи между случайными переменными и оценка её тесноты.