Линейная парная регрессия

Пусть в результате испытания получены значения случайных величин Х и Y. Экспериментальные данные удобно задавать в виде корреляционной таблицы, в которой в первом столбце представлены значения с.в. Х, а в первой строке – значения с.в. Y; числа, стоящие на пересечении строк и столбцов, показывают сколько раз наблюдалась одна и та же пара чисел (x_i, y_j).

Рассмотрим таблицу распределения пробега автомобиля Y (в км.) от количества израсходованного бензина Х (в л.).

				-	-	-
					-	-
	-					-
	-	-

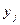
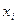
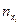
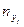
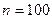
В данной таблице, например, число 3 показывает, что пара (27, 293) наблюдалась три раза, т.е. 3 автомобиля израсходовали 27 л. бензина и при этом их пробег составил 293 км. Прочерк ” - ” означает, что пара не наблюдалась. В последней строке (столбце) указана сумма чисел, расположенных во внутренних клетках по столбцам (строкам).

Символами 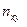будем обозначать числа во внутренних клетках, 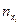- количество (частота) автомобилей израсходовавших 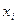л. бензина, 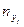- количество (частота) автомобилей, пробег которых составляет 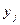км.

В нижнем правом углу указана сумма всех частот .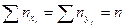

Замечание. В случае интервального статистического распределения с.в.и в качестве 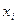, 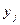выбирают середины интервалов; 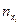, 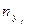- частоты попадания случайной величины в данные интервалы.

Корреляционная таблица показывает, что с увеличением объема израсходованного бензина Х пробег автомобиля имеет тенденцию к повышению. Для более точного рассмотрения этой закономерности рассмотрим групповые средние:

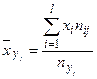и .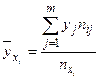

Вычислим групповые средние для нашего распределения.

.

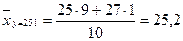
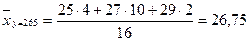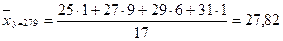
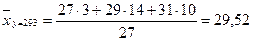
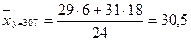
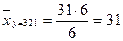
Результаты вычислений поместим в таблице:

у
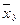
	25,2	26,75	27,82	29,52	30,5

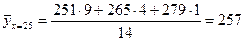
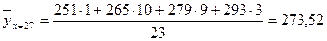
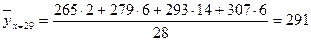
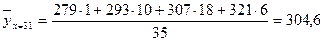
Результаты вычислений поместим в таблице:

х
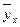
		273,52		304,6

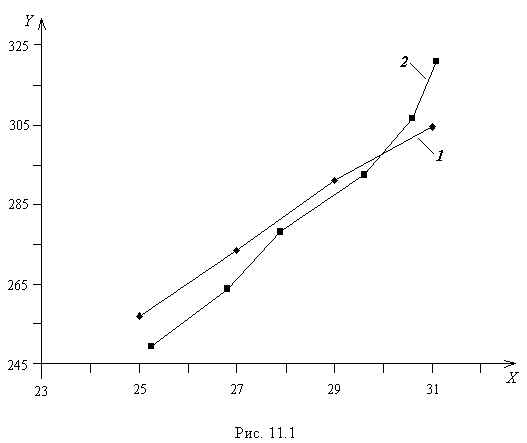
На рис. 11.1 построим графики ломаных, соединив точки с координатам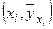и и .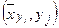

Определение. Эмпирической линией регрессии по называется ломаная, соединяющая точки с координатами 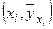. Эмпирической линией регрессии по называется ломаная, соединяющая точки с координатами .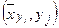

По виду ломаных (рис. 11.1) можно предположить наличие линейной корреляционной зависимости по (ломаная 1) и по (ломаная 2) между рассматриваемыми переменными.

Поставим задачу найти уравнения этих линий называемые теоретическими линиями регрессии.

Будем искать уравнение регрессии по в виде

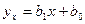. (11.1)

Неизвестные параметры 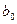и 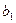выберем таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних 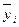от значений 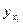, найденных по уравнению (11.1) 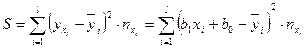, была минимальной.

Исследуем функцию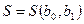на минимум.

Т.к. функция 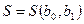является функцией двух переменных, то необходимым условием существования экстремума является равенство нулю частных производных:

.

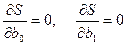Вычислим частные производные и приравняем их нулю:

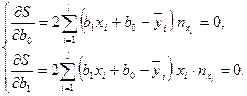
Преобразовав и разделив каждое уравнение системы на n, получим

систему нормальных уравнений: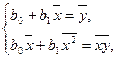

где , , , .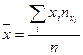

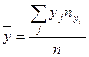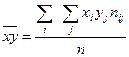Решив эту систему, найдем искомые параметры:

, .

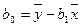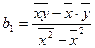Определение. Угловой коэффициент 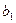прямой линии регрессии по называют коэффициентом регрессии по и обозначают :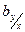

.

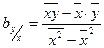Числитель 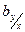: 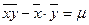- называется выборочной ковариацией.

Знаменатель 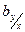: 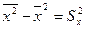- называется выборочной дисперсией .

Т.о. теоретическая линия регрессии по имеет вид: 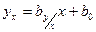. (11.2)