Преобразования Галилея. Принцип относительности Галилея. Рассмотрим две инерциальные систем системы отсчета (рис

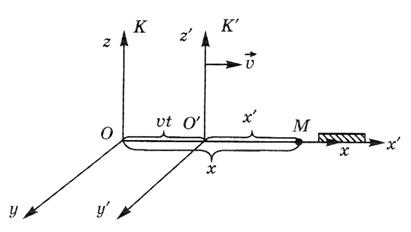
Рассмотрим две инерциальные систем системы отсчета (рис. 4.3) – неподвижную К с осями координат Ох, Оу, Оzи движущуюся относительно ее с постоянной скоростью 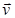вдоль совпадающих осей Ох и О^'х^' систему отсчета К^' (оси Оу и О^'у^', Ozи O^'z^' при движении остаются параллельными). В начальный момент времени (t = 0) начала координат этих систем отсчета – точки О и О^' совпадают.

В классической механике считается, что предельная скорость передачи взаимодействия в природе может быть бесконечно большой (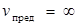), что приводит к дополнительным свойствам пространства и времени: пространство и время абсолютны, не связаны друг с другом; время течет одинаково во всех ИСО (t= t^'). Указанные свойства пространства и времени, возникающие в классической физике, позволяют получить преобразования Галилея – это формулы, связывающие координаты и время одного и того же события в разных ИСО. Под событием понимается любое явление, происходящее в одной точке пространства в какой-либо момент времени.

Пусть в точке М (рис. 4.3) происходит какое либо событие, координаты и время которого в СОК (x, y, z, t), а в СОК^' – (x^', y^', z^'. t^'). Учитывая расположение точки М и дополнительные свойства пространства и времени запишем преобразования Галилея:

Переход из К ^' в К: Переход из К в К ^':

x= x^' + vt x^' = x- vt

y= y^', z= z^' y^' = y, z^' = z

t= t^' t^' = t

В заключение отметим важный принцип относительности Галилея, существенно упрощающий описание механических явлений в разных ИСО. Он является следствием опытных фактов и утверждает равноправие всех ИСО по отношению к происходящим в них механическим явлениям.

Приведем различные эквивалентные формулировки этого принципа относительности: