Пси функция

Волнова́я фу́нкция (функция состояния, пси-функция) — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния квантовомеханической системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

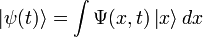
где 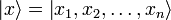— координатный базисный вектор, а 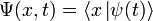— волновая функция в координатном представлении.

Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния.

В координатном представлении волновая функция 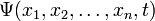зависит от координат (или обобщённых координат) системы. Физический смысл приписывается квадрату её модуля 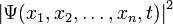, который интерпретируется как плотность вероятности 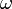(для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами 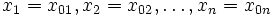в момент времени :

.

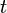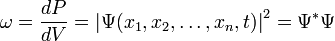Тогда в заданном квантовом состоянии системы, описываемом волновой функцией 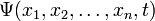, можно рассчитать вероятность 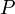того, что частица будет обнаружена в любой области пространства конечного объема :

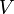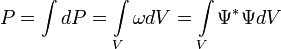
Волновая функция 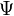по своему смыслу должна удовлетворять так называемому условию нормировки, например, в координатном представлении имеющее вид:

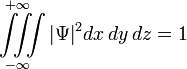
Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией где-либо во всём пространстве равна единице. В общем случае интегрирование должно производиться по всем переменным, от которых зависит волновая функция в данном представлении.