I. Разрыв первого рода

Классификация точек разрыва функции

Кроме непрерывности функции в точке рассматривают также одностороннюю непрерывность.

Определение 1. Функция непрерывна слева в точке , если определена в этой точке и некоторой левой полуокрестности точки и

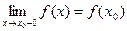. (1)

Определение 2. Функция непрерывна справа в точке , если она определена в этой точке и некоторой правой полуокрестности этой точки и

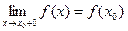. (2)

Непрерывность, описанная определениями 1 и 2 называется односторонней непрерывностью функции в точке.

Определение 3. Функция непрерывна в точке , если она определена в этой точке и некоторой ее окрестности и если

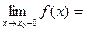
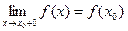
Если нарушается хотя бы одно условие определения 3, то функция имеет разрыв в точке .

В зависимости от того, какое условие определения 3 нарушено, дают классификацию точек разрыва:

1. Допустим, что в точке функция имеет равные (конечные) односторонние пределы, которые не равны значению функции в точке , т.е.

.

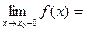
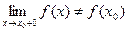В этом случае точка называется точкой устранимого разрыва.

Если функцию доопределить значением 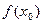равным односторонним пределам или изменить ее значение на такое, то разрыв устраняется и функция становиться непрерывной.

2. Допустим, что в точке существуют конечные неравные односторонние пределы:

, , .

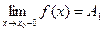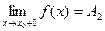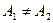В этом случае точка называется точкой конечного разрыва. Величина 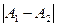называется скачком функции в точке разрыва.

Такой разрыв устранить невозможно, т.к. нарушено условие того, что это график функции.