Преобразование одномерного закона распределения случайного сигнала нелинейным безинерционным элементом

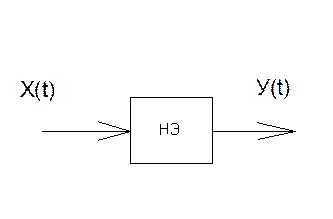
В математике подобная задача формулируется как нахождение закона распределения функционального преобразования случайной величины.

При решении этой задачи возможны три случая:

1) Обратная зависимость x=x(y) существует неоднозначно, то есть каждому значению y соответствует единственное и вполне определенное значение х.

dx, dy – бесконечно малые приращения.

Вероятность попадания у в интервал от у до у+dy равна вероятности попадания х в интервал от х до х+dx.

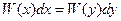
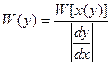(1) – решение задачи.

2) Обратная зависимость х=х(у) существует, но не однозначно, то есть каждому значению у соответствуют несколько вполне определенных значений х.

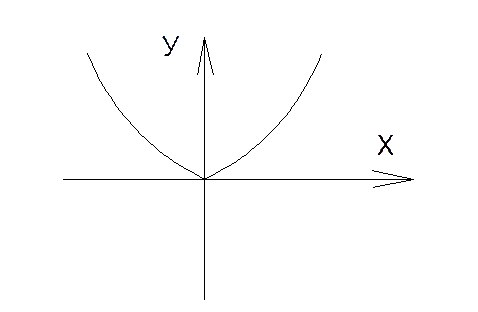
Вероятность попадания у в интервал от у да у+dy равна сумме вероятностей попадания х в соответствующие интервалы:

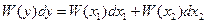
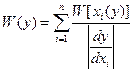(2)

3) Для некоторых значений у обратная зависимость х=х(у) не существует. Эти значения у будем называть особыми точками.

Эти значения у будем называть особыми точками.

Пример:

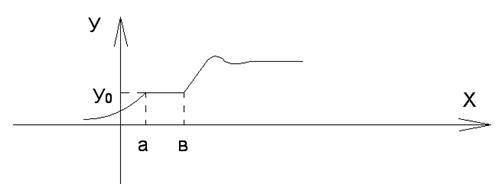
Во всех точках у, кроме у₀, W(y) находится либо по формуле (1) либо (2).

Для особой точки:

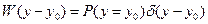(3)

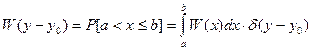
Примеры:

1)

1) Гауссовский нормальный закон.

,

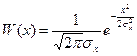
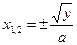
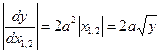
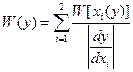
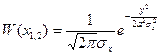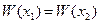
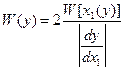
Экспоненциальный закон.

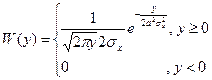
2)

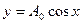
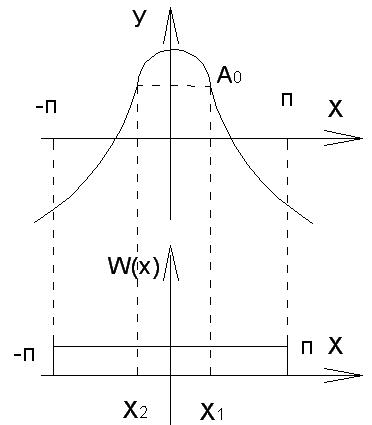
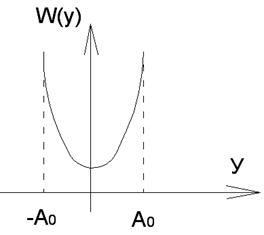
Равномерный закон распределения.

,

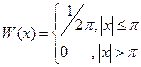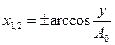
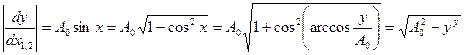
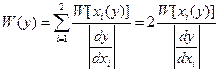
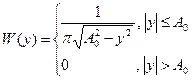
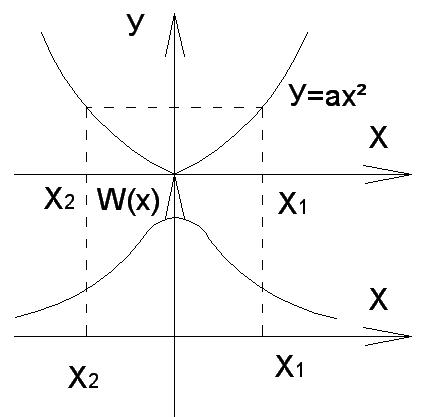
3)

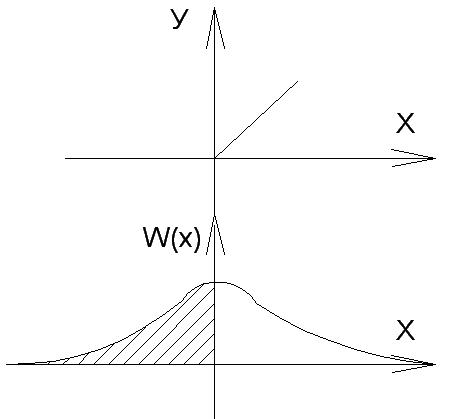
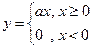
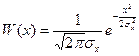
Выделим три области значения у:

- y<0: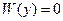

- y>0: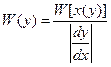

;

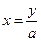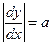
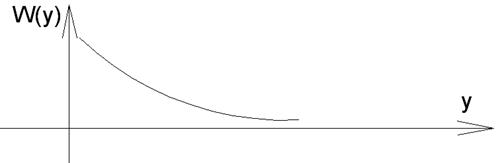
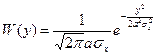– гауссовский закон распределения

-y=0:

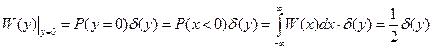
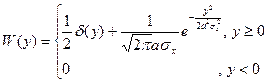
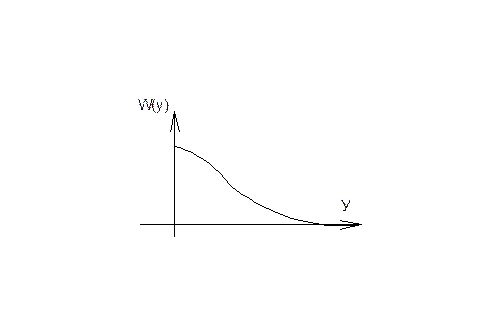
4)

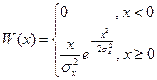
Релеевский закон распределения: