Как показано в известной литературе: плотность вероятности реализации белого гауссовского шума X(t) на интервале времени от нуля до TC можно записать в виде выражения:
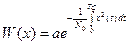 (10)
(10)
где а –постоянный множитель.
N0 - спектральная плотность белого шума.
Реализация:
x(t)=u(t)-As(t)
Если:
A=0, то x(t)=u(t)
A=1, то x(t)=u(t)-s(t)
Обозначим:
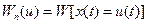
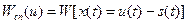
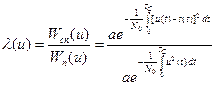
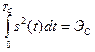 - энергия сигнала, выделяемая на единичном сопротивлении.
- энергия сигнала, выделяемая на единичном сопротивлении.
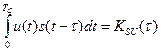 - взаимно корреляционная функция сигнала и реализации воздействия.
- взаимно корреляционная функция сигнала и реализации воздействия.
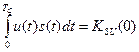 - значение взаимно корреляционной функции сигнала и реализации воздействия в момент
- значение взаимно корреляционной функции сигнала и реализации воздействия в момент  .
.
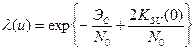
Критерий оптимальности обнаружения:
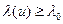
Т.к. экспонента – монотонная функция, то 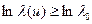
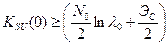
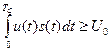
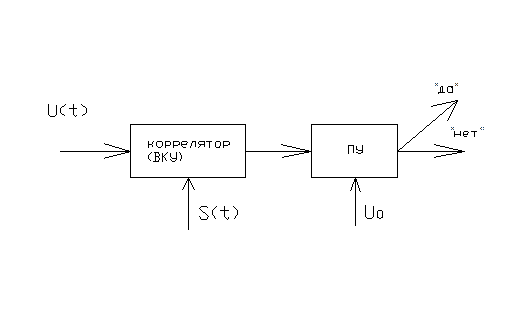
Последнее выражение в рамочке означает, что оптимальный обнаружитель полностью известного сигнала должен вычислять взаимно корреляционную функцию s(t) и реализацию воздействия и сравнить полученный результат с некоторым порогом U0.
Структура такого оптимального обнаружителя, называемого корреляционным обнаружителем, имеет вид:
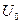 определяется энергией сигнала
определяется энергией сигнала 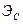 , спектральная плотность белого шума
, спектральная плотность белого шума 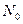 , стоимостью ошибок и вероятностями присутствия или отсутствия сигнала.
, стоимостью ошибок и вероятностями присутствия или отсутствия сигнала.
Можно расшифровать схему:
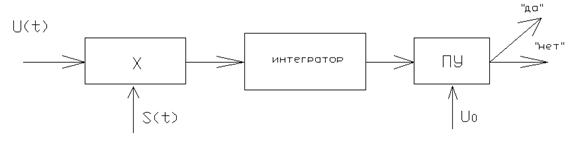
Две последние схемы корреляционного обнаружителя справедливы для полностью известного сигнала, включая ожидаемое время прихода.
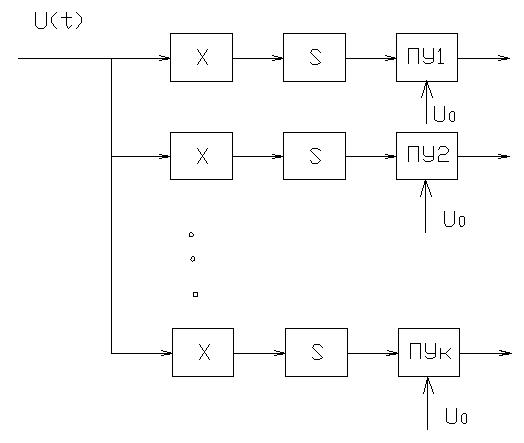
Если все параметры сигнала, кроме возможного времени прихода, известны и известен примерный диапазон значений времени прихода 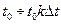
 2014-02-09
2014-02-09 2448
2448
