Дана система уравнений
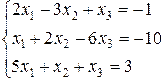
Расширенная матрица системы имеет вид:
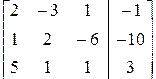 .
.
Прямой ход метода Гаусса.
На первом шаге прямого хода из второй строки вычитаем первую, умноженную на коэффициент 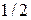 , а из третьей строки вычитаем первую, умноженную на
, а из третьей строки вычитаем первую, умноженную на 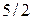 . Результат первого шага:
. Результат первого шага:
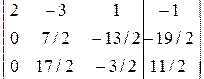 .
.
На втором шаге прямого хода из третьей строки вычитаем вторую, умноженную на 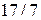 . Результат второго шага:
. Результат второго шага:
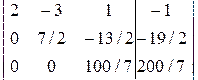 .
.
Обратный ход метода Гаусса.
Эквивалентная система с треугольной матрицей:
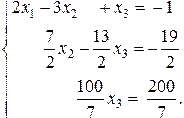
Из третьего уравнения находим:
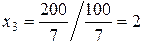 .
.
Из второго уравнения находим:
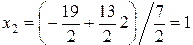 .
.
Из первого уравнения находим:
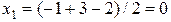 .
.
Решение рассматриваемой СЛАУ:
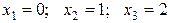 .
.
2.2.7. Пример вычисления обратной матрицы 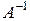 .
.
Пусть задана матрица
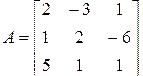
Соответствующая расширенная матрица:
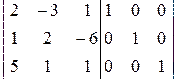 .
.
Прямой ход метода Гаусса по всей расширенной матрице.
Первый шаг:
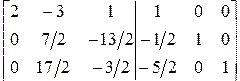 .
.
Второй шаг:
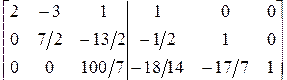 .
.
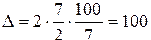 .
.
Обратный ход по каждой правой части расширенной матрицы для вычисления элементов обратной матрицы.
Вычисляем элементы первого столбца обратной матрицы:
– из третьего уравнения
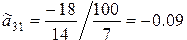 ;
;
– из второго уравнения
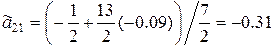 ;
;
– из первого уравнения
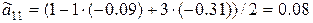 .
.
Вычисляем элементы второго столбца обратной матрицы:
– из третьего уравнения
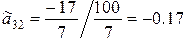 ;
;
– из второго уравнения
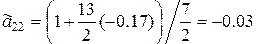 ;
;
– из первого уравнения
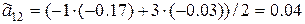 .
.
Вычисляем элементы третьего столбца обратной матрицы:
– из третьего уравнения
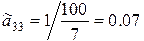 ;
;
– из второго уравнения
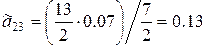 ;
;
– из первого уравнения
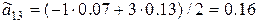 .
.
Обратная матрица имеет вид:
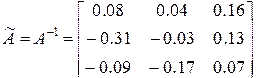 .
.
 2014-02-09
2014-02-09 1032
1032








