Метод Зейделя и метод простой итерации

Пусть задана система уравнений:

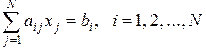. (2.3.5)

Выразим 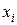через остальные члены i -го уравнения:

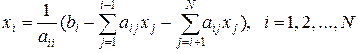. (2.3.6)

Полученная запись СЛАУ приводит к двум итерационным процессам.

Метод простой итерации.

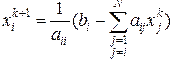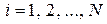, . (2.3.7)

Метод Зейделя.

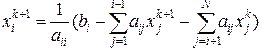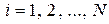, (2.3.8)

При этом 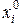задается (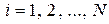), 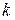– номер итерации.

Процесс ведется до выполнения условия .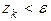

Норму 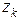вектора 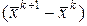можно, в частности, вычислять по формулам:

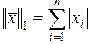1. – норма по модулю;
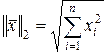2. – «евклидова» норма;
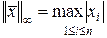3. – максимум модуля для элементов вектора.

Разница методов состоит в том, что в методе простой итерации новые значения 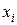учитываются лишь после вычисления их для всех 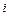, а в методе Зейделя они учитываются сразу же после вычисления их для каждого .

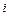При решении итерационными методами встает вопрос сходимости получаемых приближений к решению задачи.

Достаточный условие сходимости обоих методов состоит в выполнении условия диагонального преобладания:

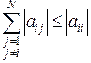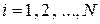, , (2.3.9)

где, по крайней мере, одно неравенство является строгим ().